Une permutation arbitraire $\sigma$ des entiers de 1 à 2012 peut être représentée dans le plan par un ensemble de 2012 points de la forme $(k,\sigma(k))$, $k$ allant de 1 à 2012. Le plus petit carré qui contient tout ces points et a ses côtés parallèles aux axes a au moins 2 et au plus 4 des points de l'ensemble sur sa frontière. Déterminer le nombre de permutations qui ont exactement $m$ points de l'ensemble sur la frontière, pour $m = 2, 3, 4$.

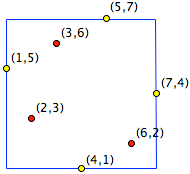
Par exemple, Le graphe de la permutation $(5,3,6,1,7,2,4)$ des entiers de 1 à 7 est l'ensemble $(1,5), (2,3), \ldots, (7,4)$ représenté dans la figure suivante. Le plus petit carré avec côtés parallèles aux axes qui contient tous ces points a exactement quatre des points sur sa frontière.

Soit $I$ le point d'intersection des trois bissectrices intérieures d'un triangle. Démontrer qu'une droite assant par $I$ divise le périmètre du triangle en deux
parties égales si et seulement si elle divise l'aire du triangle en deux parties égales.

Est-ce qu'on peut arranger les seize chiffres de la liste

$$2,2,3,3,4,4,5,5,6,6,7,7,8,8,9,9 $$

pour former deux nombres $A$, $B$ de huit chiffres, tels que $B = 2 A$ ?

Notez bien: Ne soumettez votre solution que si elle est élégante et évite les longues études de cas par cas.

On peut se réchauffer en arrangeant les douze chiffres de la liste

$$ 1,1,2,2,4,4,5,5,7,7,8,8 $$

pour former deux nombres $A$, $B$ de six chiffres, tels que $B = 2 A$ (sans nous soumettre la solution de ce réchauffement).

Déterminer s'il existe une fonction bornée $f$ à valeurs réelles
telle que $f(1) > 0$ et
$$\left(f(x+y)\right)^2 \ge \left(f(x)\right)^2 + 2f(xy) +\left(f(y)
\right)^2.$$
pour tous réels $x$ et $y$.

Le polynôme à coefficient réels $p(x)$ a degré 2011, et pour tout entier $n,\; 0 \le n \le 2011$, on a
$$p(n)=\frac{n}{n+1}.$$
Évaluer $p(2012)$.

Trouver tous les premiers $p$ tels que $\large \frac{2^{p-1} -1}{p}$ est un carré.

1. Existe-t-il une famille de cercles telle que tout point du plan est sur exactement deux des cercles?

2. Existe-t-il une famille de cercles telle que tout point du plan est sur exactement 100 des cercles?

N.B. On parle bien de cercles et non de disques, et les rayons doivent être positifs.

Déterminer le plus petit entier positif $n$ tel que $n^2 + 3n + 5$ est divisible par 121, ou démontrer qu'aucun entier ne satisfait cette condition.

Trouver les entiers positifs $m$ et $n$ pour lesquels les racines des équations
$$x^2 - mx + (n+1) = 0 \quad \mbox{ et } \quad x^2 - (n+1)x + m = 0$$
sont des entiers positifs qui, avec $m$ and $n$ constituent une progression arithmétique dont la somme est $21$ .