Solution au problème d'avril 2012

Le problème:
	Soit $I$ le point d'intersection des trois bissectrices intérieures d'un triangle. Démontrer qu'une droite assant par $I$ divise le périmètre du triangle en deux parties égales si et seulement si elle divise l'aire du triangle en deux parties égales.

Nous avons reçu les solutions correctes de

Voici la solution de Bernard Collignon:

"La droite qui passe par $I$ coupe les deux autres côtés, par exemple et
sans perte de généralité, le côté $[AC]$ en $M$ et le côté $[AB]$ en $N$ : elle partage donc le triangle $ABC$ en deux, d’un côté le triangle $MAN$ et de l’autre
le quadrilatère $BCMN$.

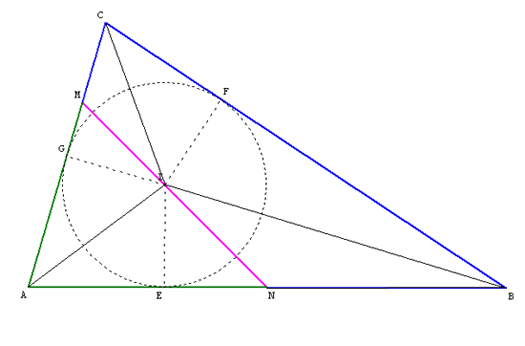
On peut procéder directement par équivalences.

La droite $MN$ divise le triangle $ABC$ en deux parties de même périmètre

$\Leftrightarrow MA + AN = NB + BC + CM$

$\Leftrightarrow IG \times MA + IE \timesAN = IE \times NB + IF \times BC + IG \times CM$

$\Leftrightarrow r \times MA + r \times AN = r \times NB + r \times BC + r \times CM$

$\Leftrightarrow \mbox{aire} ( IMA ) + \mbox{aire} ( IAN ) = \mbox{aire} ( INB ) + \mbox{aire} ( IBC ) + \mbox{aire} ( ICM )$

$\Leftrightarrow \mbox{aire} ( MAN ) = \mbox{aire} ( BCMN ) = \mbox{aire} ( ABC )/2$.''

Humbert propose la généralisation suivante:

"Soit $I$ le centre de la sphère inscrite dans un tétraèdre non aplati $ABCD$. Soit $P$ un plan passant par $I$. $P$ divise $ABCD$ en deux morceaux, de volumes respectifs $V_1$ et $V_2$, et d'aires extérieures (c'est-à-dire hors de $P$) respectives $A_1$ et $A_2$.

On a : $A_1/A_2 = V_1/V_2$''

Voici sa démonstration :

"Le tétraèdre $ABCD$ est l'union des quatre petits tétraèdres $ABCI$, $ABDI$, $ACDI$ et $BCDI$. Considérons l'un de ces petits tétraèdres, disons $ABCI$, qui est coupé en deux

morceaux par $P$. $P$ coupe deux des trois arêtes du triangle de base $ABC$, disons $[AB]$ en $M$ et $[AC]$ en $N$.

Les deux morceaux de $ABCI$ sont des pyramides de hauteur le rayon $r$ de la sphère inscrite dans $ABCD$ donc :

$$\mbox{Volume}(AMNI) = r/3 \mbox{Aire}(AMN)$$

$$\mbox{Volume}(BCNMI) = r/3 \mbox{Aire}(BCNM) .$$

En procédant de même pour les autres petits tétraèdres, puis en additionnant les contributions de chaque morceau à $V_1$ et $A_1$ ou à $V_2$ et $A_2$, on obtient:

$V_1 = r/3 A_1$ et $V_2 = r/3 A_2$, donc finalement $A_1/A_2 = V_1/V_2$. ''

Il note que ce raisonnement est valable en toute dimension $n ≥ 2$ :

"Soit $S$ un $n$-simplexe non aplati et $I$ le centre de son hypersphère inscrite. Soit $P$ un hyperplan passant par $I$. $P$ divise le $n$-simplexe en deux morceaux $S_1$ et $S_2$, dans le même rapport des $n$-volumes et des $(n-1)$-volumes extérieurs (c'est-à-dire hors de $P$).''

En dimension 2, Fondanaiche démontre qu'il existe nécessairement un segment passant par $I$ et divisant le périmètre du triangle (ou bien l’aire du triangle) en deux parties égales :

"Soit $M$ un point courant du périmètre du triangle $ABC$, par exemple sans perte de généralité, sur le côté $BC$. La droite $MI$ coupe un deuxième côté du triangle en un point $N$ situé sur $AC$ (voir figure supra) ou $AB$, ce qui permet de construire le vecteur $\vec{MN}$. On désigne par $f(M)$ la différence algébrique entre la longueur $MCN$ et la longueur $NABM$ mesurées l’une et l’autre dans le sens anti-horaire.Il est facile de vérifier que lorsque $M$ se déplace le long du périmètre du triangle, le vecteur $\vec{MN}$ pivote autour de $I$ et $f(M)$ varie continûment.

Or $f(N) = – f(M)$. Le théorème des valeurs intermédiaires (voir http://fr.wikipedia.org/wiki/Théorème_des_valeurs_intermédiaires ) nous permet alors de dire qu’il existe un point $P$ du périmètre du triangle $ABC$ tel que $f(P) = 0$.

Le même raisonnement peut être tenu avec le partage du triangle en deux zones de même aire. En effet la fonction $g(M)$ égale à la différence des deux aires est elle aussi une fonction continue qui prend deux valeurs de signes opposés en $M$ et $N$ et à laquelle peut s’appliquer le théorème des valeurs intermédiaires.''

En fait, Campo Ruiz et Desprez ont démontré qu'il existe exactement une, deux ou trois de ces droites passant par $I$ qui sépare le périmètre et l'aire en deux parties égales.

Commentaires. Dans une lettre à l'éditeur, Anthony Todd [Letter to the Editor, Mathematics Magazine, 84 : 5 (Dec. 2011) 396] note qu'il a appris l'existence de ce problème dans [Alexander Shen, Entrance Examinations to the Mekh-mat, The Mathematical Intelligencer, 16 : 4 (1994) 6-10; disponible au site
http://www.3038.org/press/shen.pdf]. L'article décrit la discrimination envers certains groupes ethniques à l'examen d'entrée au Mekh-mat de l'Université de Moscou dans les années 1970 et 1980. Un des problèmes difficiles qui était conçu pour éilminer plusieurs des membres de ces groupes, était de tracer une droite qui bissecte l'aire et le périmètre d'un triangle. Nous avons vu que l'existence d'une telle droite est facile à établir. Par contre, il est beaucoup plus difficile de construire une telle droite. Une telle construction est donnée dans [Saturnino Campo Ruiz, Solución Problema 138 http://www.aloj.us.es/rbarroso/trianguloscabri/sol/sol138sat.htm]. La lettre de Todd contient d'autres références intéressantes dont son site web
http://www.math.colostate.edu/info/applets/bisect_triangle/bisect_triangle.html contenant un applet qui coustruit la droite recherchée. D'autres commentaires sont disponibles sur notre page anglaise.