Solution au problème de novembre 2011

Le problème:
	Existe-t-il une famille de cercles telle que tout point du plan est sur exactement deux des cercles? Existe-t-il une famille de cercles telle que tout point du plan est sur exactement 100 des cercles? N.B. On parle bien de cercles et non de disques, et les rayons doivent être positifs.

La solution:

Le problème provient du Tournoi des villes de 1988 en France; la question était alors de couvrir chaque point par 1988 cercles. Il est paru plus tard dans le livre Hypermath: 120 exercices de haut vol de Pierre Bornsztein (Vuibert, Paris, 2001). Merci à Jean Doyen qui nous a communiqué le problème.

Nous avons reçu les solutions correctes de Lamis Alsheikh (Syrie), Bernard Collignon (France), Philippe Fondanaiche (France), Jan Fricke (Allemagne), Benoît Humbert (France), Ile Ilijevski (Macédoine), et Patrick J. LoPresti (États Unis). La réponse est oui aux deux questions. Nos correspondants utilisaient tous essentiellement la même construction de réseaux parallèles de cercles. Selon Humbert, pour la question a, l'ensemble des cercles de diamètre 1 et de centre ayant une abscisse entière fait l'affaire. Collignon représente ainsi cette solution.

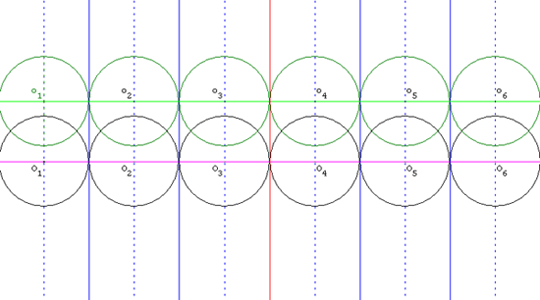
Il note que dans une solution, les réseaux de cercles n'ont pas besoin d'avoir le même rayon; il suffit que la distance entre deux réseaux consécutifs soit égale à la somme des rayons correspondants.

Pour la question b, il suffit de combiner 50 solutions de la question a. Selon Humbert, l'ensemble de tous les cercles de diamètre 1 et de centre ayant une abscisse multiple de 1/50 fait l'affaire. Cette construction se généralise bien sûr, permettant de recouvrir le plan par des cercles de telle sorte que tout point est sur exactement $N$ cercles pour tout $N$ pair. Humbert note qu'on ne peut recouvrir le plan par des cercles disjoints:

"Esquisse de la preuve (par l'absurde) : sinon il existe une suite de cercles, chacun strictement à l'intérieur du précédent, convergeant vers un point n'appartenant pas aux cercles de cette suite. Le cercle auquel appartient ce point coupe nécessairement certains cercles de cette suite, ce qui est interdit. (Problème et réponse trouvés dans le livre de Paul Halmos, Problèmes pour mathématiciens, petits et grands)''

On ne sait pas si il existe un recouvrement du plan par des cercles de telle sorte que tout point est sur exactement $N$ cercles pour $N$ impair et supérieur à 1.