Solution au problème de mai 2012

Le problème:

Une permutation arbitraire $\sigma$ des entiers de 1 à 2012 peut être représentée dans le plan par un ensemble de 2012 points de la forme $(k,\sigma(k))$, $k$ allant de 1 à 2012. Le plus petit carré qui contient tout ces points et a ses côtés parallèles aux axes a au moins 2 et au plus 4 des points de l'ensemble sur sa frontière. Déterminer le nombre de permutations qui ont exactement $m$ points de l'ensemble sur la frontière, pour $m = 2, 3, 4$. Par exemple, Le graphe de la permutation $(5,3,6,1,7,2,4)$ des entiers de 1 à 7 est l'ensemble $(1,5), (2,3), \ldots, (7,4)$ représenté dans la figure suivante. Le plus petit carré avec côtés parallèles aux axes qui contient tous ces points a exactement quatre des points sur sa frontière.

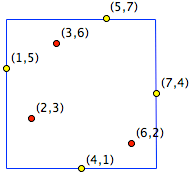
Nous avons reçu les solutions correctes de

Notre problème de ce mois est un cas particulier du Problème 1862 de Mathematics Magazine, proposé par Emeric Deutsch. On trouve la. solution à ce problème dans le volume 85, No. 1 (févriere 2012) à la page 63 : Les graphes des $n!$ permutations des entiers de 1 à $n$ comportent

Dans le cas $n = 2012$, nos correspondants nous fournissent les arguments suivants.

2 points sur la frontière. Voici l'argument de Collignon:

"Il faut dans ce cas que les deux points soient situés sur deux sommets opposés du carré, ce qui correspond aux deux familles de permutations telles que :

$\sigma(1) = 1$ et $\sigma(2012) = 2012$ et donc aux sommets $(1,1)$ et $(2012,2012)$

ou bien $\sigma(1) = 2012$ et $\sigma(2012) = 1$ et donc aux sommets $(1,2012)$ et $(2012,1)$.

Il reste donc 2010 points à placer à l’intérieur du carré, ce qui correspond à $2 \times 2010!$ permutations au total.

3 points sur la frontière.Voici l'argument de Humbert :

"Il y a quatre coins possibles, puis 2010 positions possibles pour le point du côté vertical opposé, puis $2010!$ permutations possibles des nombres restants. Au final, il y a $4 \times 2010 \times 2010!$ permutations pour lesquelles le carré contient trois points.

4 points sur la frontière. Voici l'argument de Notarantonio :

"Cela correspond aux graphes de permutations suivants :

$$\sigma : (a, ...., b)$$

avec $a \neq1$ et $a \neq2012$, et $b \neq 1$ et $b \neq 2012$. Il y a 2010 emplacements différents pour l'entier 1 (puisqu'il ne peut pas être à l'emplacement 1 ou à l'emplacement 2012), et ensuite 2009 emplacements différents pour l'entier 2012 (puisqu'il ne peut pas être à l'emplacement 1 ou à l'emplacement 2012 ou à l'emplacement où 1 a été placé). Il reste 2010 entiers à placer dans les 2010 emplacements restant: cela correspond à $2010!$ permutations différentes.

On a donc $2009\times 2010 \times 2010!$ permutations qui ont exactement 4 points de l'ensemble sur la frontière.''

On peut aditionner ces valeurs pour vérifier qu'elles sont consistantes:

$$\begin{eqnarray*}
2&\times& 2010! + 4 \times 2010 \times 2010! + 2010 \times 2009 \times 2010! \\&=&
(2+2013\cdot 2010) \times 2010!\\ &=& (2012\times 2011) \times 2010! = 2012!,
\end{eqnarray*}$$

tel qu'il se doit.