|
MP60: mai 2006
Quel est le plus grand diviseur commun des 1003 nombres
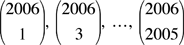 ? ?
(Où 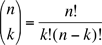 est le nombre de groupes de k objets qu'on peut former à partir d'un ensemble de n objets.) est le nombre de groupes de k objets qu'on peut former à partir d'un ensemble de n objets.)
Solution au problème de mai 2006
MP59: avril 2006
Deux joueurs A et B choisissent à tour de rôle un des 9 coefficients ai du polynôme
x10 + a9 x9 + a8 x8 + a7 x7 + a6 x6 + a5 x5 + a4 x4 + a3 x3 + a2 x2 + a1 x + 1
et le remplacent par un réel de leur choix. Le jeu se termine après 9 coups, lorsque les valeurs de tous les ai sont connues. Le premier joueur A gagne si le polynôme obtenu n'a aucune racine réelle. Le second joueur B gagne si le polynôme a au moins une racine réelle. L'un des deux joueurs peut s'arranger pour être toujours gagnant, quoi que fasse son adversaire. De quel joueur s'agit-il?
Solution au problème de avril 2006
MP58: mars 2006
Jean écrit au tableau noir un nombre de 2187 chiffres, dont chaque chiffre est un 1 ou un 2. Judith crée un nouveau nombre à partir de celui de Jean: elle lit le nombre de gauche à droite, et chaque fois qu'elle lit un 1 elle écrit 112, et chaque fois qu'elle lit un 2 elle écrit 111. (Par exemple, si le nombre de Jean commence par 2112, celui de Judith commence par 111112112111.) Après avoir terminé, Judith réalise que les 2187 premiers chiffres de son nombre (en commençant par la gauche) forment exactement le nombre de Jean. Combien de fois rencontre-t-on la séquence 11111 dans le chiffre de Jean?
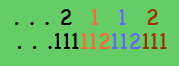
Solution au problème de mars 2006
MP57: février 2006
Deux équations quadratiques de la forme
x2 - bx + c = 0 et x2 - bx - c = 0,
où b et c sont entiers, constituent une paire compatible si elles ont toutes deux des solutions entières. Par exemple
x2 - 5x + 6 = 0 a pour solutions x = 2 et x = 3, tandis que
x2 - 5x - 6 = 0 a pour solutions x = -1 et x = 6.
En multipliant b par d et c par d2 on obtient une nouvelle paire compatible x2 - bdx ± cd2= 0; une paire compatible est dite primitive si b et c n'ont aucun diviseur commun. Existe-t-il d'autres paires compatibles primitives?
Solution au problème de février 2006
MP56: janvier 2006
Bonne et heureuse année. L'équipe du Problème du Mois vous souhaite pour l'année à venir tout le bonheur et la bonne santé dont vous avez profité l'année dernière:
Déterminez le maximum de f(2006)-f(2005), où f est une fonction à valeurs réelles telle que
|f(x) - f(y)| ≤ (x-y)2
pour tous nombres réels x et y.
Solution au problème de janvier 2006
MP55: décembre 2005
Les aiguilles de ma montre tournent toutes selon un mouvement circulaire uniforme, sans à-coup. A l'instant précis où la trotteuse (qui indique les secondes) passe sur une des 12 subdivisions du cadran, je sais que dans moins d'une demi-seconde, la grande aiguille passera exactement sur la petite. Quelle heure est-il, sachant qu'il n'est pas encore midi ?
Solution au problème de décembre 2005
MP54: novembre 2005
Le professeur Adam entre en classe et écrit au tableau noir un polynôme f(x) à coefficients entiers. Il dit ensuite "C'est aujourd'hui l'anniversaire de mon fils, et lorsqu'on évalue f à son âge A, on a f(A) = A. Notez aussi que f(0) = p, où p est un nombre premier supérieur à A." Quel âge a le fils du professeur Adam?
Solution au problème de novembre 2005
MP53: octobre 2005
Le premier joueur lance une pièce de monnaie 1001 fois, et le deuxième joueur 1000 fois. Quelle est la probabilité que le premier joueur obtienne pile plus souvent que le deuxième?
(Vous êtes priés d'éviter les calculs monstrueux)
Solution au problème de octobre 2005
MP52: septembre 2005
Notre premier problème de l'année porte sur les nombres. En guise de réchauffement, vous pouvez commencer par démontrer que pour tout nombre n impair, (4n + 1) est un multiple de 5. Notre question est la suivante:
Démontrez que pour tout entier n impair et supérieur à 3, 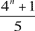 est un nombre composé. est un nombre composé.
Solution au problème de septembre 2005
| 
