Jean écrit au tableau noir un nombre de 2187 chiffres, dont chaque chiffre est un 1 ou un 2. Judith crée un nouveau nombre à partir de celui de Jean: elle lit le nombre de gauche à droite, et chaque fois qu'elle lit un 1 elle écrit 112, et chaque fois qu'elle lit un 2 elle écrit 111. (Par exemple, si le nombre de Jean commence par 2112, celui de Judith commence par 111112112111.) Après avoir terminé, Judith réalise que les 2187 premiers chiffres de son nombre (en commençant par la gauche) forment exactement le nombre de Jean. Combien de fois rencontre-t-on la séquence 11111 dans le chiffre de Jean?
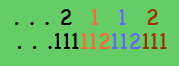
A la mi-février de chaque année, des étudiants de la neuvième a la onzième année de partout au Canada participent aux coucours mathématiques de l'Université de Waterloo. Notre problème du mois était la question finale du concours Pascal (pour la neuvième année) de février dernier.
Nous avons reçu des solutions correctes de
| Vincent Bardoux (France) | Wolfgang Kais (Allemagne) | |
| Mohamed Benchaib (Maroc) | Karim Laaouini (Maroc) | |
| Pierre Bornsztein (France) | Normand LaLiberté (Ontario) | |
| Bernard Carpentier (France) | Matthew Lim (internet) | |
| K.A. Chandrashekara | Juan Mir Pieras (Espagne) | |
| Philippe Fondanaiche (France) | Mark Pilloff (États-Unis) | |
| Xavier Hecquet (France) | A. Teitelman (Israël) | |
| LeCarré de l'Hypoténuse (France) | Said Amghibech (internet) |
Solution.
La chaîne 11111 apparait 182 fois dans le chiffre de Jean.
La plupart de nos correspondants sont arrivés à cette conclusion à partir d'observations similaires. Nous reproduisons ici la solution de Normand LaLiberté.
Solution de Normand LaLiberté
On rencontre 182 fois la séquence 11111 dans le chiffre de Jean.
Résultats préliminaires concernant la somme de séries géométriques alternées.
Soit S( 2n + 1) = r2n - r2n-1 + r2n-2 - ... - r + 1
Nous avons:
r S( 2n + 1) = r2n+1 - r2n + r2n-1 - ... - r2 + r
d'où:
S( 2n + 1) + r S( 2n + 1) = r2n+1 + 1
d'où:
S( 2n + 1) = (r2n+1 + 1) / (r + 1)
De la même manière, on montre:
Si T( 2n) = r2n - 1 - r2n- 2 + r2n-3 - ... + r - 1
alors T( 2n) = (r2n - 1) / (r + 1)
Revenons au nombre de Jean; il ne peut commencer avec 2; autrement, celui de Judith commencerait avec 112 et serait alors différent de celui de Jean. Non seulement le nombre de Jean commence avec 1 mais avec 112. Ceci, en conjonction avec les règles de réécriture: 1 -> 112, 2 -> 111, signifie que le nombre de Jean est le même que celui obtenu en commençant avec le chiffre 1 puis en appliquant répétitivement les deux règles ci-dessus. Ainsi, on construit une suite de nombres; la longueur de chaque nombre est une puissance de 3. Convenons que le 1 initial soit au niveau 0 -les espaces dans le tableau suivant sont utilisés pour améliorer la lisibilité.
Quelques remarques:
1.Les règles de réécriture impliquent que le nombre de 2 au niveau n est égal au nombre de 1 au niveau n - 1.
|
niveau
|
nombre
|
nombre de 2 = nombre de 1 au niveau n - 1
|
| 0 | 1 | 0 |
| 1 | 112 | 30 |
| 2 | 112 112 111 |
31 - 30
|
| 3 | 112 112 111 112 112 111 112 112 112 |
32 -(31 - 30)
|
| 4 | ... |
33 -(32 -(31
- 30))
|
| 5 | ... |
34 -(33 - (32
-(31 - 30)))
|
Ainsi, on obtient le nombre de Jean au niveau 7; sa longueur est 37 = 2187.
Soit N( n) = nombre de 2 au niveau n
La 3ième colonne du tableau montre que N( n) est une série géométrique alternée de raison 3. Une preuve formelle par induction basée sur le fait que N( n) = 3n-1 - N( n - 1) est facile; aussi, n'est-elle pas incluse.
D'après les résultats préliminaires ci-haut:
N( 2n) = (32n - 1) / (3 + 1),
N( 2n + 1) = (32n+1 + 1) / (3 + 1).
Soit M( n) = nombre de séquences 11111 au niveau n
D'après la 3ième remarque ci-dessus:
M( n) = N( n - 1) si n est impair
D'où:
M( 7) = N( 6) = (36 - 1) / (3 + 1) = 728 / 4
QED
Autres commentaires.
La règle de réécriture du nombre de Jean a une
conséquence intéressante: Si au niveau k on dénote
A et B les blocs initial et final de 3k-1 chiffres, alors la
chaîne de 3k chiffres est de la forme AAB, et au niveau
suivant la chaîne est de la forme AAB AAB AAA (tout comme on passe
de 112 à 112 112 111). De plus, à chaque niveau le
nombre de 2 est à moins d'une unité du quart des chiffres.
Malgré ces motifs réguliers dans la suite de chaînes,
Mir note que la chaîne limite infinie n'est pas périodique
— si une chaîne de p chiffres à partir du d-ième
se termine par 1, alors la chaîne de 3p chiffres à partir
du 3d-ième se termine par 2 et vice-versa. Mir note que certaines
règles de réécriture produisent des chaînes
périodiques; par exemple remplacer 1 par 121 et 2 par 212.
Enfin, Hecquet nous a envoyé le nombre de Jean au complet pour le bénéfice de ceux qui voudraient compter par eux-mêmes le nombre de 11111 et vérifier que nos correspondants ont raison.
Le nombre de Jean:
112112111112112111112112112112112111112112111112112112112112111112112111112
112111112112111112112111112112112112112111112112111112112112112112111112112
111112112111112112111112112111112112112112112111112112111112112112112112111
112112111112112112112112111112112111112112112112112111112112111112112112112
112111112112111112112111112112111112112111112112112112112111112112111112112
112112112111112112111112112111112112111112112111112112112112112111112112111
112112112112112111112112111112112112112112111112112111112112112112112111112
112111112112112112112111112112111112112111112112111112112111112112112112112
111112112111112112112112112111112112111112112111112112111112112111112112112
112112111112112111112112112112112111112112111112112111112112111112112111112
112112112112111112112111112112112112112111112112111112112111112112111112112
111112112112112112111112112111112112112112112111112112111112112111112112111
112112111112112112112112111112112111112112112112112111112112111112112112112
112111112112111112112112112112111112112111112112112112112111112112111112112
111112112111112112111112112112112112111112112111112112112112112111112112111
112112111112112111112112111112112112112112111112112111112112112112112111112
112111112112112112112111112112111112112112112112111112112111112112112112112
111112112111112112111112112111112112111112112112112112111112112111112112112
112112111112112111112112111112112111112112111112112112112112111112112111112
112112112112111112112111112112111112112111112112111112112112112112111112112
111112112112112112111112112111112112111112112111112112111112112112112112111
112112111112112112112112111112112111112112111112112111112112111112112112112
112111112112111112112112112112111112112111112112112112112111112112111112112
112112112111112112111112112112112112111112112111112112111112112111112112111
112112112112112111112112111112112112112112111112112111112112111112112111112
112111112112112112112111112112111112112112112112111112112111112112112112112
111112112111112112112112112111112112111112112112112112111112112111112112111
112112111112112111112112112112112111112112111112112112112112111112112111112
112111112112111112112111112112112112112111112112111112112112112112111112112
111112112112
Problèmes et solutions précédents