Les aiguilles de ma montre tournent toutes selon un mouvement circulaire uniforme, sans à-coup. A l'instant précis où la trotteuse (qui indique les secondes) passe sur une des 12 subdivisions du cadran, je sais que dans moins d'une demi-seconde, la grande aiguille passera exactement sur la petite. Quelle heure est-il, sachant qu'il n'est pas encore midi ?
Nous avons reçu des solutions correctes de
Vincent Bardoux (France) |
Aleksandar Ilic (Serbie et Montenegro) |
|
Bernard Carpentier (France) |
Wolfgang Kais (Allemagne) |
|
Philippe Fondanaiche (France) |
Matthew Lim (internet) |
|
Xavier Hecquet (France) |
Juan Mir Pieras (Espagne) |
|
| Wilfrid Pillard (France) |
Solution.
L'aiguille des heures et celle des minutes se déplacent chacune à une vitesse constante, donc un intervalle de temps constant sépare les instants où elles se superposent. Les deux aiguilles se superposent onze fois dans un cycle de douze heures (à minuit juste, puis une fois entre une heure et deux heures, une fois entre deux heures et trois heures, et ainsi de suite jusqu'à une dernière fois entre dix heures et onze heures). Ainsi, l'intervalle entre les superpositions des aiguilles est de 12/11 heures, soit en secondes (12x60x60)/11 = 3927 et 3/11 secondes, ce qui correspond à
1 heure, 5 minutes, 27 et 3/11 secondes.
Après la superposition qui a lieu à minuit juste, on note les superpositions successives dans la table suivante.
Superposition |
heure |
minute |
seconde |
1 |
1 |
5 |
27 + 3/11 |
2 |
2 |
10 |
54 + 6/11 |
3 |
3 |
16 |
21 + 9/11 |
4 |
4 |
21 |
49 + 1/11 |
5 |
5 |
27 |
16 + 4/11 |
6 |
6 |
32 |
43 + 7/11 |
7 |
7 |
38 |
10 + 10/11 |
8 |
8 |
43 |
38 + 2/11 |
9 |
9 |
49 |
5 + 5/11 |
10 |
10 |
54 |
32 + 8/11 |
11 |
12 |
0 |
0 |
Lorsque la trotteuse passe sur une des subdivisions du cadran, le nombre des secondes est un multiple de 5. Pour qu'une des superpositions énumérées ci-haut aie lieu moins d'une demi-seconde plus tard, il doit être 9 heures, 49 minutes et 5 secondes.
Tous nos correspondants nous ont donné une variation de l'argument ci-haut. Kais nous a aussi donné un deuxième argument qui utilise l'arithmétique modulaire et évite de faire une liste de toutes les superpositions. Sachant que la n-ième superposition après minuit a lieu (12/11) 
3600n secondes après minuit et que
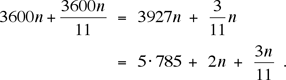
Nous cherchons les valeurs de n pour lesquelles
2n + (3n/11) dépasse par moins de ½ un multiple de 5:
5k < (2 + 3/11)n < 5k + ½.
De facon équivalente, 55k < 25n < 55k + 11/2, ou
11k < 5n < 11k + 11/10.
Puisque since 5n et 11k sont des entiers, on a 5n = 11k + 1. Nous cherchons une valeur de n entre 1 et 11 telle que 5n 
1 (mod 11). L'inverse multiplicatif de 5 (mod 11) est -2 11 - 2 = 9 (mod 11). Puisque 5 et 11 sont relativement premiers, n 9 (mod 11) est la seule solution. L'heure recherchée est donc la partie entière de (12/11)x3600x9 secondes après minuit, soit 9 heures, 49 minutes et 5 secondes.
Problèmes et solutions précédents