|
Solution au problème de septembre 2010
| Le problème: |
 |
MP97
Problème de septembre 2010
Un plombier a une pile de tuyaux de même longueur, et une boîte de raccords en coude à angle droit. Il se rend compte qu'il ne peut pas les utiliser pour former un pentagone, mais qu'il peut former des polygones à six et à sept côtés. Démontrer que le plombier a raison.
(On ne peut pas connecter les tuyaux directement ensemble. Il faut toujours utiliser un coude pour connecter deux tuyaux, et donc former un angle droit.)
Nous avons
reçu des solutions correctes de
Bojan Basic (Serbie) |
Verena Haider (Autriche) |
Bernard Collignon (France) |
Benoît Humbert (France) |
Shai Covo (Israël) |
Matthew Lim (États Unis) |
Mei-Hui Fang (Autriche) |
Patrick J. LoPresti (États Unis) |
Philippe Fondanaiche (France) |
John T. Robinson (États Unis) |
Bruce Golfman (Autriche) |
Albert Stadler (Suisse) |
Cornel Gruian (Roumanie) |
|
|
La solution:
Certains disent qu'il suffit de le voir pour le croire. Par contre, les
mathématiciens savent qu'on ne peut pas croire tout ce qu'on
voit:

Triangle de Penrose dans un parc de Gotschuchen, Autriche
Photo reproduite des fichiers de Wikipedia.
Nous reproduisons la solution de
Fondanaiche.
Q1 :
Il est impossible de former un pentagone avec cinq tuyaux.
Si
une solution existe, à l’évidence on ne peut pas
l’obtenir dans le plan mais seulement dans l’espace à
trois dimensions.
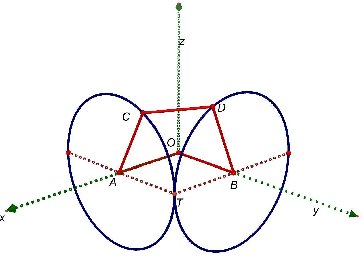
Les
deux
premiers tuyaux OA et OB de longueur unité appartiennent au
plan horizontal. Le lieu de l’extrémité C du
troisième tuyau AC est le cercle de centre A et de rayon
unité
situé dans le plan perpendiculaire à OA tandis que le
lieu de l’extrémité D du tuyau BD est le cercle de
centre B et de rayon unité situé dans le plan
perpendiculaire à OB. Il s'agit de trouver un segment CD de
longueur unité perpendiculaire à la fois à AC et
à BD. On désigne par (x,y,z) les coordonnées de
C et par (x’,y’z’) celles de D avec x = 1 et y’ = 1.On a les
cinq équations suivantes :
- C
est sur le
cercle de centre A et de rayon unité : y2 + z2 = 1
- D
est sur le
cercle de centre B et de rayon unité : x'2 + z'2 = 1
- CD
est de
longueur unité : (1 - x')2 + (y - 1)2 + (z - z')2 = 1
- CD
est
perpendiculaire à AC : y(1 – y ) + z(z’ – z) = 0
- CD
est
perpendiculaire à BD : x’(x’ – 1) + z’(z’ –
z) = 0
Cinq
équations
pour quatre inconnues : il y a une équation en trop !
Des trois premières, on déduit par exemple x’ + y +
zz’ = 1 et des deux dernières : y +zz’ = 1 et x’ +
zz’ = 1. D’où x’ = y = 0 ce qui entraîne d’après
1) et 2) z = z’ = 1 qui est incompatible avec 3)
Q2 : Il est possible de former deux polygones de six et sept tuyaux
respectivement comme le montre la figure ci-après (vue en
perspective)
Là
encore, il n’y a pas de solution dans le plan*** mais dans l’espace
à trois dimensions.
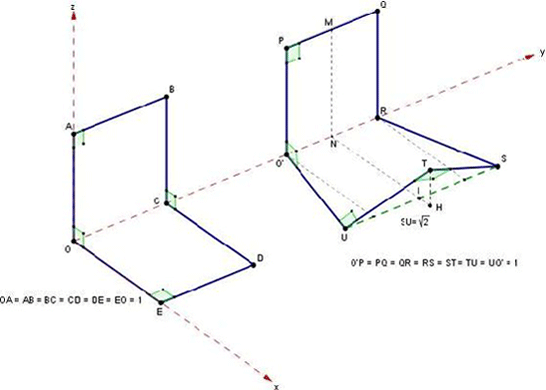
Le montage à six tuyaux est très simple
à
obtenir avec les trois premiers tuyaux (OA,AB,BC) raccordés
entre eux pour former un « U » qui appartient
à un plan vertical et les trois derniers tuyaux (CD,DE,EO)
raccordés de la même manière pour former un
deuxième U appartenant à un plan horizontal
perpendiculaire au précédent. Les deux
« U »
sont raccordés aux points O et C de telle sorte que AO est
perpendiculaire à OE et BC est perpendiculaire à CD.
Le montage
à
sept tuyaux se déduit du précédent de la
manière suivante : les trois premiers tuyaux O’P,PQ et
QR sont placés comme les tuyaux OA,AB et BC dans le plan
vertical.On place les 4ième et 5ième
tuyaux O’U et RS dans le plan horizontal de telle sorte que O’U
= RS = 1 et US = 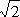 , U et S étant
symétriques l’un de l’autre par rapport au plan MNI
médiateur de O’PQR. Le point T qui est l’extrémité
commune aux 6ième et 7ième tuyaux
est le sommet du triangle rectangle isocèle STU. Il est donc
situé sur le cercle (γ) situé dans le plan MNI,
centré au milieu I de SU et
de rayon , U et S étant
symétriques l’un de l’autre par rapport au plan MNI
médiateur de O’PQR. Le point T qui est l’extrémité
commune aux 6ième et 7ième tuyaux
est le sommet du triangle rectangle isocèle STU. Il est donc
situé sur le cercle (γ) situé dans le plan MNI,
centré au milieu I de SU et
de rayon 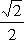 . Le
tuyau TU étant perpendiculaire à O’U est dans le plan
perpendiculaire à O’U passant par U.Ce plan coupe le cercle
(γ)
en
deux points dont le point T représenté sur la figure
ci-dessus. En raison des positions symétriques de U et de S
par rapport au plan MNI, TS est aussi perpendiculaire à RS.
Soit H la projection de T sur le plan horizontal.On a les distances
suivantes : . Le
tuyau TU étant perpendiculaire à O’U est dans le plan
perpendiculaire à O’U passant par U.Ce plan coupe le cercle
(γ)
en
deux points dont le point T représenté sur la figure
ci-dessus. En raison des positions symétriques de U et de S
par rapport au plan MNI, TS est aussi perpendiculaire à RS.
Soit H la projection de T sur le plan horizontal.On a les distances
suivantes :
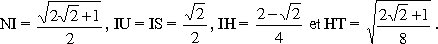
On
peut
prolonger les montages à 8 et 9 tuyaux en remplaçant
les tuyaux AB et PQ par trois tuyaux raccordés en forme de U
et situés dans des plans respectivement perpendiculaires aux
plans OABC et O’PQR.L’extension à 2k et 2k+1 tuyaux ( k
>4 ) se fait de la même façon.
En
conclusion, seul le montage à 5 tuyaux est impossible.
*** Des
solutions dans le plan existent avec 4, 12, 20, ...tuyaux qui donnent
un carré, une croix grecque,etc...
Commentaires.
La source de ce problème est le problème 1110 (proposé par Gerald
Wildenberg) dans Mathematics Magazine, 55 (1982) 47-48.
|

