|
Solution au problème d'octobre 2008
| Le problème: |
 |
Trouvez la plus
longue suite possible d'entiers où la somme de sept
termes consécutifs est toujours positive, et la somme de onze
termes
consécutifs est toujours négative.
|
La solution:
Nous avons reçu des solutions correctes de
| Bojan Basic
(Serbie) |
Matthew Lim (États-Unis) |
Gérard Billion (France) |
John T. Robinson (États-Unis) |
Lou Cairoli (États-Unis) |
K. Sengupta (Inde) |
Sébastien Dumortier (France) |
Javier Rodríguez Soler (Espagne) |
| Philippe
Fondanaiche (France) |
Albert Stadler
(Suisse) |
Farid Lian Martínez (Colombie) |
|
Notre problème d'octobre
est une version modifiée du problème 2 de l'Olympiade
Internationale de Mathématiques de 1977 (voir International
Mathematical Olympiads 1959-1977, édité par Samuel L.
Greitzer; Mathematical Association of America, New Mathematical Library
No. 27, 1978).
Solution. Toute
suite obéissant aux deux conditions
(1) la somme de 7
termes consécutifs est toujours positive
et
(2) la somme de 11 termes
consécutifs est toujours négative
a au plus 16 termes. En effet, supposons une suite a1,
a2, ..., a17 obéissant aux deux conditions.
Considérons le tableau suivant.
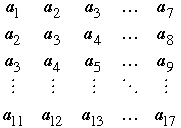
Selon la condition (1), la somme des termes sur chaque
ligne est positive, et selon (2) la somme des termes sur chaque colonne
est négative, donc la somme de tous les termes du tableau est
à la fois positive et négative, ce qui est impossible.
Il reste à vérifier qu'il existe bien une
suite de 16 termes obéissant aux deux conditions. Billion y
parvient en inversant la matrice correspondant au système d'inéquations:
"Appelons
X le vecteur colonne
dont les composantes sont égales
successivement aux n termes de la suite. Soit S le vecteur colonne
dont les composantes sont égales successivement au 10 sommes
de 7 termes puis au 6 sommes de 11 termes. Nous avons la relation
matricielle S=MX, avec M la matrice ci-dessous, et par
recombinaison
on peut trouver la matrice inverse M-1,
et ainsi pour
tout S on peut calculer X = M-1
S.
M = 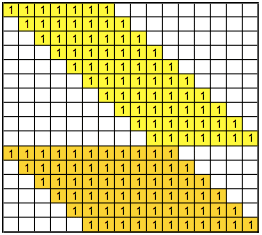 ,
M-1 =  . .
Si on donne par exemple à S la valeur (1,1,1,1,1,1,1,1,1,1,-1,-1,-1,-1,-1,-1) on trouve pour X (-5, -5,13, -5, -5, -5, 13, -5, -5, 13, -5, -5, -5,13, -5, -5). Cette suite de 16 entiers est telle que la somme de sept termes consécutifs est toujours positive (+1), et la somme de onze termes consécutifs est toujours négative (-1). Si on donne par exemple à S la valeur (2, 2, 2, 2, 2, 2, 2, 2, 2, 2,-3,-3,-3,-3,-3,-3) on trouve également pour X (-12, -12,31, -12, -12, -12, 31, -12, -12, 31, -12, -12, -12,31, -12, -12).''
Ainsi, la solution de Billion démontre qu'il est possible de fixer n'importe quelles valeurs positives pour les sommes de sept termes consécutifs, et n'importe quelles valeurs négatives pour les sommes de onze termes consécutifs.
Basic donne une solution alternative démontrant qu'on peut trouver une solution en fixant les sommes partielles S0 = 0, S1 = a1, S2 = a1 + a2, ..., S16 = a1 + a2 + ... + a16 de façon consistante. Les conditions (1) et (2) correspondent respectivement aux inégalités Si < Si+7 et Si > Si+11, ce qui donne la chaîne
S6 < S13 < S2 < S9 < S16 < S5 < S12 < S1 < S8 < S15 <S4 < S11< 0
< S7 < S14 < S3 < S10.
Il suffit donc de choisir des valeurs consistantes pour les termes Si pour ensuite déterminer les termes ai = Si - Si-1. Cette approche permet de généraliser l'énoncé (comme l'ont fait Basic, Fondanaiche, Lim, et Sengupta), et démontrer que la longueur maximale d'une suite où la somme de m termes consécutifs est toujours positive et la somme de n termes consécutifs est toujours négative est m + n - PGCD(m,n) - 1.
|

