Nous
avons reçu des solutions correctes de
Saïd Amghibech (Québec) |
|
Wolfgang Kais (Allemagne) |
Mario Antunez (Honduras) |
|
Normand LaLiberté
(Ontario) |
Ricardo Barroso Campos (Espagne) |
|
Matthew Lim (États-Unis) |
Pierre Bornsztein (France) |
|
Juan Mir Pieras (Espage) |
Bernard Carpentier (France) |
|
Nikhil V. Nair (Inde) |
K.A. Chandrashekara (India) |
|
Wilfrid Pillard (France) |
Stefaan De Winter (Belgique) |
|
Mark Pilloff (États-Unis) |
Sébastien Dumortier (France) |
|
Manoranjan Sahu (Inde) |
Philippe Fondanaiche (France) |
|
Shiv Mohan Sharma (internet) |
Baptiste Gorin (France) |
|
A. Teitelmam (Israël) |
Xavier Hecquet (France) |
|
Zac Friggstad (Alberta) |
La plupart de nos correspondants se sont contentés d'une
solution directe. Nous présentons cette solution, suivie d'une
simplification suggerée par Saïd Amghibech. La suite
elle-même est liée à quelques idées de
Gauss; nous conclurons avec son approche au problème, incluant
sa preuve par deus ex machina.
La solution directe. Puisque nous utilisons
seulement six termes de la suite, remplacons an, ... , an+5 respectivement par u, v, w, x, y, z. Avec cette notation nous avons les
quatre équations
(1) uw = v+1, (2) vx =
w+1, (3) wy = x+1, (4)
xz = y+1,
et nous devons démontrer que z = u.
De (1) nous obtenons 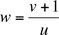 .
.
Nous substituons cette valeur de w dans (2), et continuons de la
même manière pour obtenir successivement
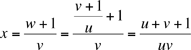
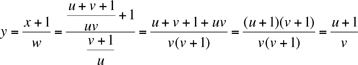
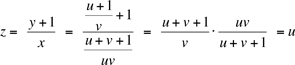
Nous avons donc z = u, c'est à dire an+5 = an pour tout n, tel
qu'annoncé.
Notons que puisque tous les termes sont positifs, notre
approche est bien valide puisqu'il n'y a aucune division par
zéro. Mir note qu'il suffit en fait de stipuler que a0 + 1 ≠ 0 , a1 + 1 ≠ 0, et a0 + a1 + 1 ≠
0.
Une simplification de Saïd Amghibech (un
peu modifiée).
Avec la notation de la première solution, multiplions
l'équation (4) par w pour obtenir
wxz =(4) wy + w =(3) x +
1 + w =(2) x + xv = x(1 + v) =(1) xuw
En simplifiant wx des deux côtés, nous
obtenons z = u.
On trouve une autre
simplification en notant que la condition est symétrique en n+1
et n-1; la formule est la même pour n croissant que pour n
décroissant, ce qui incite à commencer par le millieu.
Posons an = w et an+1 = x. Nous avons alors
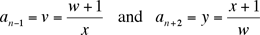
dont on déduit (comme dans la première solution)
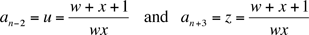
Par conséquent an-2 = an+3 pour tout n, ce qui est une
autre façon de dire que la suite est un 5-cycle.
La solution de Gauss.
Gauss n'a pas daigné nous envoyer sa solution. Nous l'avons
plutôt obtenue de l'article "Frieze Patterns", Acta
Arithmetica 26 (1971), pages 297-310 de H.S.M.
Coxeter.
Selon Coxeter, l'histoire
commence en 1602, lorsque Nathaniel Torporley (1564-1632) commence
à étudier les 5 "parties" a, A, b, B, c d'un triangle
rectangle sphérique (avec l'angle C droit). Selon De Morgan,
Torporley anticipa d'une douzaine d'années les règles de
Napier qui figurent dans le pentagramma mirificum de
Gauss. Ces règles permettent de déduire beaucoup de
trigonométrie sphérique sans trop d'effort. Gauss
se servit de l'identité
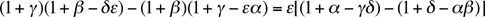
pour démontrer que n'importe quelles trois
des relations

implique la quatrième et aussi 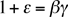 .
.
Le centre du pentagramme est un
pentagone dont les sommets sont des pôles des cinq arcs, c'est
donc un pentagone auto-polaire. ce qui veut
dire que si un des sommets du pentagone est placé au pôle
nord, le côté opposé est à
l'équateur. On peut développer toute la figure à
partir du triangle ABC (au haut de la figure) en prolongeant
les côtés et en tracant aussi les grand cercles polaires
de A et B. Notons x' le complément de x:
x' = 1/2 π - x ,
ainsi les côtés du
pentagone auto-polaire sont
A, B, b', c, a'
et les autres arcs et angles sont
tels qu'indiqués dans la figure. Toute équation
connectant les cinq "parties" (ainsi modifiées) demeure valide
lorsqu'elles sont permutées cycliquement. C'est là
l'observation de Napier (sauf qu'il utilisait le cycle alterné a',
B, c, A, b').
Gauss posa
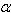 = tan2 A,
= tan2 A,
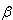 = tan2 B,
= tan2 B,
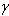 = tan2 b',
= tan2 b',
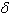 = tan2 c,
= tan2 c,
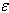 = tan2 a'
= tan2 a'
et se servit des relations classiques (telles que cos c = cot A cot B) pour obtenir
sec2 A = 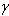
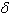 ,
sec2 B =
,
sec2 B = 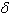
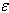 ,
sec2 b' =
,
sec2 b' = 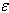
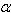 ,
,
sec2 c = 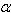
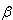 ,
sec2 a' =
,
sec2 a' = 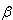
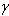 .
.
Notons que ces
relations impliquent 1 +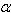 =
= 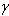
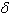 , et ainsi de suite. Coxeter donne d'autres
explications et applications, en particulier à la
trigonométrie du plan hyperbolique; mais nous terminons ici
notre récit.
, et ainsi de suite. Coxeter donne d'autres
explications et applications, en particulier à la
trigonométrie du plan hyperbolique; mais nous terminons ici
notre récit.

