|
Solution au
problème de décembre 2006
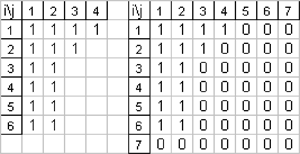
On désigne par p(n) la partition initiale du tas de n pièces en s piles ordonnées p1, p2,...,ps tels que p1 + p2 + ... + ps = n et p1 ≥ p2 ≥ ... ≥ ps ≥ 1 .
Cette partition peut se représenter sous la forme d’un tableau à double entrée rempli de 1 tel que dans la première colonne les p1 pièces sont identifiées par p1 chiffres 1 alignés les uns en dessous des autres sur p1lignes, …,puis dans la j-ième colonne les pj pièces sont représentées par pj chiffres 1 alignés les uns en dessous des autres sur pj lignes, etc…. On remplit ensuite le tableau avec des 0 de manière à obtenir un tableau carré dont la plus grande diagonale Sud-Ouest / Nord-Est contient au moins un chiffre1.
Par exemple pour n=15 et p(15) = (6,6,2,1), cela donne les tableaux suivants dont le deuxième est de dimension (7x7):
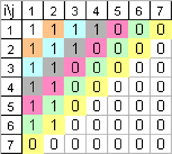
Dans la suite de la démonstration, on va s’intéresser à toutes les diagonales orientées SO  NE qui contiennent au moins un chiffre 1. Elles sont représentées ci-après avec différentes couleurs : NE qui contiennent au moins un chiffre 1. Elles sont représentées ci-après avec différentes couleurs :
On appelle T[p(n)] le tour qui consiste à prendre une pièce de chaque pile pour former une nouvelle pile de s pièces. On obtient au plus s +1 piles et le nombre de piles est ramené à s+1-u avec u nombre de piles de la partition initiale constituées d’une seule pièce. La pile qui a le plus grand nombre de pièces contient max[p1 - 1, s] pièces.
T[p(n)] peut être décomposé en deux opérations bien distinctes:
-
T1[p(n)] qui consiste à effectuer à l’intérieur de chacune des diagonales orientées SO  NE qui contiennent au moins un chiffre 1, une permutation circulaire des chiffres qu’elle contient toujours dans le sens SO NE qui contiennent au moins un chiffre 1, une permutation circulaire des chiffres qu’elle contient toujours dans le sens SO 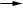 NE. NE.
Avec l’exemple de la partition p(15) précédemment décrite, on obtient ainsi un nouveau tableau toujours de dimension (7x7):
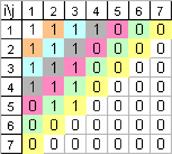
On observe qu’on obtient 4 piles : trois d’entre elles sont les piles d’origine dont on a extrait une pièce et se retrouvent en 2ème, 3ème et 4ème colonnes. Elles contiennent respectivement 5,5 et 1 pièces. La pile d’une pièce qui était en 4ème colonne à l’origine a disparu. La quatrième pile de la nouvelle partition se trouve en 1ème colonne et contient 4 pièces. On obtient ainsi la configuration (4,5,5,1) dans laquelle les piles sont non ordonnées.
-
T2[p(n)] qui consiste à décaler d’un cran vers la gauche du tableau les chiffres 1 (s’ils existent) qui se trouvent dans les 2ème, 3ème,…colonnes et sur les lignes s+1, s+2,….de manière à faire apparaître une nouvelle partition dans laquelle tous les effectifs des piles n°1,2,3,…sont dans un ordre non croissant.
Le tableau précédent devient alors :
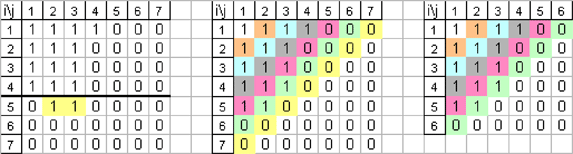
Après suppression de la 7ème diagonale qui ne contient que des 0, la nouvelle partition ordonnée est représentée par la séquence (5,5,4,1) à l’intérieur du troisième tableau de dimension (6x6).
On désigne par T(i)[p(n)] la répétition i fois du tour qui consiste à prélever une pièce de chaque pile pour en créer une nouvelle. Comme le nombre de partitions d’un entier quelconque n est fini, on est assuré que par répétition de T autant de fois que nécessaire, on retombera sur une partition déjà observée. On dit alors que la partition q(n) est T-cyclique s’il existe un entier i tel que
T(i)[p(n)] = q(n) .
On va démontrer le théorème suivant et son corollaire :
Théorème : soit un entier n quelconque qui peut s’écrire sous la forme
n = 1 + 2 + 3 +…+ (k-1) + r avec 1 ≤ r ≤ k.
Alors p(n) est T-cyclique si et seulement si p(n) est de la forme
( k-1+ ak-1, k-2+ ak-2,…, 2+ a2,1 + a1, a0) avec chaque ai qui prend la valeur 0 ou 1 et 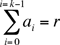
Corollaire : si n est un nombre triangulaire de la forme 1 + 2 + ….+k = k(k+1)/2, alors (k, k-1, k-2,….,2,1) est l’unique T-cyclique partition de n.
Démonstration :
Si p(n) est de la forme ( k-1+ ak-1, k-2+ ak-2,…, 2+ a2, 1 + a1, a0), on vérifie aisément que le tableau associé à p(n) a ses (k-1) premières diagonales qui sont toutes remplies de 1, la k-ième diagonale comporte les chiffres de la séquence ai pour i variant de 0 à k-1 et au delà de cette diagonale, il n’y a que des zéros. Toute opération du type Ti[p(n)] a donc pour effet de laisser en l’état les (k-1) premières diagonales et de réaliser une permutation circulaire dans le sens
SO  NE des chiffres de la k-ième diagonale. Au bout de k permutations, on retombe ainsi sur la partition initiale et l’on a T(k)(p(n)] = p(n). La partition p(n) est bien cyclique : NE des chiffres de la k-ième diagonale. Au bout de k permutations, on retombe ainsi sur la partition initiale et l’on a T(k)(p(n)] = p(n). La partition p(n) est bien cyclique :
Exemple n = 13 avec la partition initiale (5,3,2,2,1), on a les tableaux successifs suivants :

A cette occasion, on constate que T1[p(n)] conserve chaque chiffre du tableau à l’intérieur de chacune des diagonales alors que T2[p(n)] a pour effet de décaler vers la gauche les chiffres 1, s’ils existent, qui se trouvent dans les 2ème, 3ème,…colonnes et sur les lignes s+1, s+2,…Ainsi pour toute partition qui est T-cyclique, seules les opérations de type T1[p(n)] sont effectuées.
Réciproquement on va démontrer que toute partition T-cyclique est de la forme
(k-1+ ak-1, k-2+ ak-2,…, 2+ a2,1 + a1, a0). On suppose que ce n’est pas le cas et qu’il existe une partition p(n) T-cyclique sans être de la forme précédemment définie. Dès lors il y a au moins un zéro sur la x-ième diagonale et un chiffre 1 sur la (x+1)-ième diagonale. Comme p(n) est T-cyclique, seules les opérations de type T1[p(n)] sont à effectuer. Comme les entiers x et x+1 sont premiers entre eux, il y aura au plus tard après x2 - x - 1 étapes, un tableau dans lequel le chiffre 0 sera en position (1,x) et le chiffre 1 en position (x+1,1) . A l’étape suivante, le chiffre 1 sera à droite du chiffre 0 et il sera nécessaire d’effectuer une opération du type T2[p(n)] pour mettre les piles de le nouvelle partition dans un ordre non croissant. D’où la contradiction.
Exemple : n=13 avec la partition initiale (5,5,1,1,1)
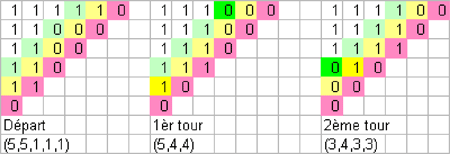
Dans la partition initiale (5,5,1,1,1), la quatrième diagonale (en vert clair) comporte un 0 en position (2,3) et la cinquième diagonale (en jaune clair) à comporte plusieurs chiffres 1.On a repéré par les couleurs jaune et vert foncé les chiffres 0 et1 qui se trouvent respectivement à l’issue du premier tour en position (1,4) et (5,1). Après le 2ème tour, le chiffre 1 est bien à droite du chiffre 0.
A partir du théorème ainsi démontré, on en déduit que :
- pour r = k, c’est à dire pout tout entier n triangulaire, on a l’unique partition T-cyclique (k,k-1,k-2,…..,2,1) qui est immuable à l’issue de chaque tour.
- n’importe quelle partition définie avec ce nombre triangulaire n et distincte de (k,k-1,k-2,…..,2,1) atteint au bout d’un nombre fini d’étapes la partition T-cycliq
Il a été démontré que le nombre d’étapes pour aboutir à la partition (k,k-1,k-2,…..,2,1) à partir de n’importe quelle partition est majoré par k2- k (voir démonstration de Jorgen Brandt).
Source : The cycling of partitions and compositions under repeated shifts- Jerrold R. Griggs and Chih-Chang Ho – May 5, 1998
|

