Solution au problème de janvier 2011

Le problème:

Selon la formule de Héron, l'aire d'un triangle est déterminée par les longueurs de ses trois côtés. Est-ce que le volume d'un tétraèdre est déterminé par les aires de ses quatre faces? Nous avons reçu les solutions correctes de Claudio Baiocchi (Italie) Benoît Humbert (France) Lou Cairoli (États Unis) Ile Ilijevski (Macédoine) Mei-Hui Fang (Autriche) Wolfgang Kais (Allemagne) Philippe Fondanaiche (France) John T. Robinson (États Unis) Bruce Golfman (Autriche) Albert Stadler (Suisse) Verena Haider (Autriche)

La solution:

Nous reproduisons la solution de Baiocchi et les commentaires Fondanaiche.

Solution de Baiocchi: ''On va montrer que la réponse est négative en s'appuyant sur la propriété isopérimétrique du tétraèdre régulier: parmi les tétraèdres de surface fixé, le volume est maximum (strict) lorsque le tétraèdre est régulier; en particulier on pourrait se borner à construire un tétraèdre non-régulier dont toutes les faces ont égale aire. On va faire un peu mieux, en construisant un tétraèdre dont les quatre faces sont égales. Trois possibilités:

1. POUR LES PLUS PARESSEUX: il suffit de remarquer que le carré $ABCD$ où $A=(-1,0), B=(0,-1), C=(1,0) \mbox{ et } D=(0,1)$ peut être vu comme un tétraèdre dont C est le sommet relatif à la base ABD. Les quatre faces sont identiques.
   
   
2. POUR CE QUI SE MÉFIENT DES DÉGÉNÉRESCENCES: par rapport au carré précédent, il suffit de rajouter la troisième dimension $z$; on soulève le côté $AC$ à une hauteur $h$ et on baisse le côté $BD$ à la hauteur $-h.$ Encore les quatre faces sont identiques et (sauf une unique valeur de $h$) le tétraèdre n'est pas régulier.
   
   
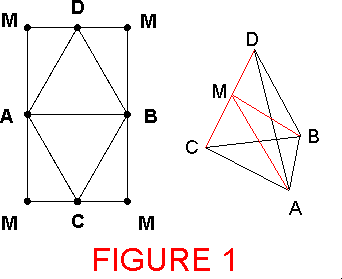
3. POUR LES ESPRITS GÉOMÉTRIQUES: il y a à peu près 13 lustres mon père me montra qu'on peut construire un tétraèdre régulier à partir d'un rectangle dont le rapport des mesures est la racine carré de 3: si $M$ est le milieu du côté $CD$, il suffit de couper le tétraèdre le long du côté $CD$ et des hauteurs $AM, BM;$ voir figure 1. Par ailleurs, partant d'un rectangle quelconque, la construction donne toujours un tétraèdre ayant les quatre faces identiques. 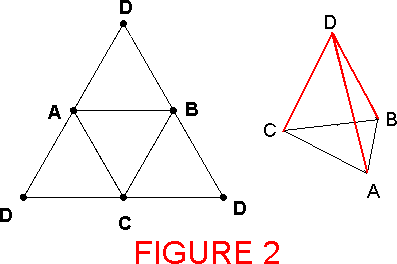Naturellement on parviendrait au même résultat à partir du développement "plus traditionnel" donné en figure 2, qui marche à partir d'un quelconque triangle isoscèle.

Commentaires de Fondanaiche: ''Il y a plusieurs façons de calculer le volume $V$ d’un tétraèdre. Le plus souvent on retient la surface d'une base $B$ du tétraèdre déterminée par trois côtés et la hauteur h du tétraèdre s'appuyant sur cette base et l’on calcule $V = B\frac{h}{3}.$ On utilise plus rarement la formule de Tartaglia due au célèbre peintre Piero della Francesca
(http://en.wikipedia.org/wiki/Tartaglia’s_formula#Volume_of_a_tetrahedron ) dans laquelle apparaissent les dimensions des six côtés $a,b,c,d,e,f.$ Le volume $V$ du tétraèdre est donnée par l’expression ci-après dans laquelle le membre de droite est égale au déterminant de la matrice $5x5:$

\[288 V^2 = \left | \begin{array}{ccccc} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & a^2 & b^2 & c^2 \\ 1 & a^2 & 0 & d^2 & e^2 \\ 1 & b^2 & d^2 & 0 & f^2\\ 1 & c^2 & e^2 & f^2 & 0 \end{array} \right |.\]

Il est exact que cette formule a un air de parenté avec celle de Héron qui donne la surface A d’un triangle dont les côtés sont $a,b \mbox{ et } c$
(voir : http://en.wikipedia.org/wiki/Heron’s_formula):

$$16 A^2 = \left | \begin{array}{ccccc} 0 & 1 & 1 & 1 \\ 1 & 0 & a^2 & b^2 \\ 1 & a^2 & 0 & c^2 \\ 1 & b^2 & c^2 & 0\end{array} \right |.$$

La similitude des formules ne permet pas pour autant de conclure que V peut s’exprimer en fonction des aires $A_1 , A_2 , A_3 , A_4$ des quatre faces du tétraèdre.''

D'autres commentaires sont disponibles sur notre page anglaise.