|
Solution au problème de décembre 2010
| Le problème: |
 |
Est-ce que (20102011!)2 est plus grand que 2010201120102011?
Nous avons reçu des solutions correctes de
| Bojan Bašić (Serbie) |
Wolfgang Kais (Allemagne) |
| Luigi Bernardini (Italie) |
Paul King (Ontario) |
| José Borges (Portugal) |
Normand LaLiberté (Ontario) |
| Lou Cairoli (États Unis) |
Matthew Lim (États Unis) |
| José David Calcines Padilla |
Remo Mantovanelli (Italie) |
| K.A. Chandrashekara (Inde) |
Nawal Kishor Mishra (Inde) |
| Bernard Collingnon (France) |
Vincent Pantaloni (France) |
| Gruian Cornel (Roumanie) |
Paolo Perfetti (Italie) |
| Shai Covo (Israël) |
Christian Pont (France) |
| Allen Druze (États Unis) |
Shpetim Rexhepi (Macédoine) |
| Mei-Hui Fang (Autriche) |
John T. Robinson (États Unis) |
| Philippe Fondanaiche (France) |
Ilir Selmani (Macédoine) |
| Paul Führmann and Nicolas Michel
(France) |
Heri Setiyawan (Indonésie) |
| Bruce Golfman (Autriche) |
Madan Mohan Singhal |
Verena Haider (Autriche)
|
Albert Stadler (Suisse) |
| Paul Hatfield (Australie) |
Todd Stohs |
| Benoît Humbert (France) |
Damian Straszak (Pologne) |
| Ile Ilijevski (Macédoine) |
A. Teitelman (Israël) |
| Kipp Johnson (États Unis) |
Paul Voyer (France) |
|
La solution:
La réponse est oui, de
beaucoup. Selon l'ordinateur de Bašić, (20102011!)2 a plus de 276 000 000 chiffres alors que 2010201120102011 a moins de 147 000 000 chiffres! Nous avons reçu plusieurs
démonstrations différentes. D. Kipp Johnson a
tellement aimé le problème qu'il nous a fait parvenir
sept solutions différentes. Nous présenterons quatre de
ses démonstrations (incorporant les idées de nos autres
correspondants) et une cinquième démonstration de Singhal
et Golfman. La première démonstration remporte le prix
pour la simplicité, et le prix pour l'originalité va
à la cinquième.
Première
démonstration: Une inégalité élémentaire
Notons d'abord que pour 1 ≤ k ≤ n,
k · (n - (k - 1)) = n + (k - 1)(n
- k) ≥ n,
avec égalité lorsque k = 1 ou k = n, et inégalité stricte lorsque 1 < k < n. Donc pour tout entier n plus grand
que 2,
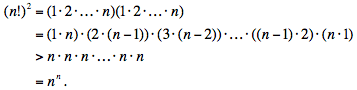
Deuxième
démonstration: L'induction.
Démontrons que (n!)2 > nn pour n ≥ 3.
On a (3!)2 = 36 et 33 = 27, donc (n!)2 > nn lorsque n = 3; c'est le cas de base.
Supposons maintenant que pour un entier k ≥ 3, on a (k!)2 > kk. Sachant que 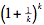 < 3 (si on ne le
sait pas, on peut consulter la démonstration ci-bas), on a k + 1
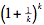> . ce qui donne la chaîne suivante
d'inégalités:
Le pas d'induction est donc complété, et
l'inégalité est démontrée pour tout n ≥ 3;
en particulier, l'inégalité est vraie pour n = 20102011.
Commentaire. Puisque 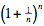 croît avec n vers e = 2.718..., la suite joue un rôle important en analyse. Par contre un argument simple suffit à démontrer que 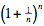< 3. Verena Haider donne l'argument
suivant, basé sur le théorème du binôme:
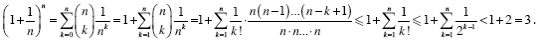
Troisième
démonstration: L'approximation
de Stirling.
Selon la version enfantine de la formule de Stirling, 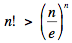 pour tout entier positif n; on peut consulter MathWorld ou
Wikipedia pour une démonstration.
Lorsque n ≥ 8 on a n > e2 , et donc
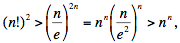
ce qui démontre que (20102011!)2 > 2010201120102011.
Quatrième
démonstration: Les
sommes de Riemann. (La version de Matthew Lim.)
Lorsque n > e2, on a ln n -2
> 0 et
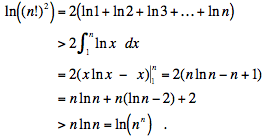
En appliquant la fonction exponentielle des deux
côtés, on obtient (n!)2 > nn pour
tout entier n ≥ 8.
(Notons que cette démonstration est en gros la même que la précédente, avec
la démonstration de la formule de Stirling intégrée.)
Cinquième
démonstration: L'inégalité
arithmético-géométrique.
La suite
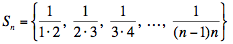
a n – 1 termes, qui sont distincts lorsque n > 2. Sa moyenne arithmétique est
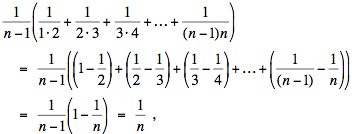
et sa moyenne géométrique est
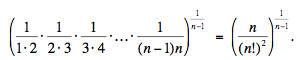
La moyenne arithmétique d'une suite de termes
distincts est toujours supérieure à sa moyenne géométrique, donc pour n > 2,
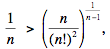
ou
|
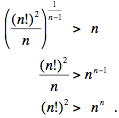
