|
Solution au problème d'avril 2011
| Le problème: |
 |
- Existe-t-il une fonction continue $f: \mathbb{ R}\rightarrow \mathbb{ R}\;$ qui prend chacune des valeurs de son image deux fois exactement?
- Existe-t-il une fonction continue $f: \mathbb{ R}\rightarrow \mathbb{ R}\;$ qui prend chacune ses valeurs de son image trois fois exactement?
La réponse:
Non à la partie (a); Oui à la
partie (b)
Nous avons reçu les solutions correctes de
Lou Cairoli (États Unis) |
Mei-Hui Fang (Autriche) |
Philippe Fondanaiche (France) |
Gruian Cornel (Roumanie) |
Tom Holens (Manitoba) |
Lars Huettenberger (Allemagne) |
Benoît Humbert (France) |
Ile Ilijevski (Macédoine) |
Kipp Johnson (États Unis) |
Omran Kouba (Syrie) |
Antek Łączkowski (Pologne) |
Matthew Lim (États Unis) |
Patrick J. LoPresti (États Unis) |
Fatemeh Naghipour (Regina) |
Paolo Perfetti (Italie) |
Shpetim Rexhepi (Macédoine) |
John T. Robinson (États Unis) |
Ignacio Somma Esteves |
Albert Stadler (Suisse) |
|
|
La solution:
Solution à la partie (a). Nous
reproduisons la solution de Fondanaiche.
"Supposons qu’il existe deux nombres réels $a$ et $b$
avec $a < b$ tels que $f(a) = f(b)$. A l’intérieur de
l’intervalle $[a,b]$, on ne peut pas avoir deux nombres $c$
et $d$ distincts tels que $f(c) > f(a)$ et $f(d) <
f(a)$. Si c’était le cas,d’après le théorème des
valeurs intermédiaires (voir http://fr.wikipedia.org/wiki/Théorème_des_valeurs_intermédiaires ) on aurait un nombre $e$ compris entre $c$ et $d$ tel que
$f(e) = f(a)$ et la valeur $f(a)$ serait prise trois fois.
D’où contradiction. Il en résulte qu’à l’intérieur
de l’intervalle $[a,b$ et pour tout $x \in [a,b]$, on a
$f(x) > f(a)$ ou bien $f(x) < f(a)$.
Sans perte de généralité,
supposons $f(x) > f(a)$.

Prenons un point $c \in [a,b]$.
Toujours d’après le théorème des valeurs intermédiaires,
$f$ qui est continue prend toutes les valeurs entre $f(a)$ et
$f(c)$ sur $[a,c]$ mais aussi sur $[c,b]$. Pour $x < a$ ou
pour $x > b$, on ne peut pas avoir $f(x) > f(a)$. Sinon
il en résulterait que $f$ prendrait ces valeurs une
troisième fois sur $[x,a]$ ou sur $[b,x]$. On a donc $f(x) <
f(a)$ pour $x$ en dehors de l’intervalle $[a,b]$.
Par conséquent la fonction $f$
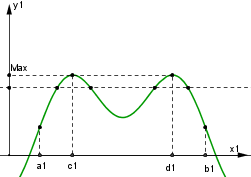
est bornée supérieurement sur $\mathbb{ R}$. Soit Max la valeur maximale. Si
cette valeur maximale est prise une fois et une seule, on est
en contradiction avec l’hypothèse initiale. La valeur Max
est alors prise deux fois. D’où
la configuration ci-dessous dans laquelle on constate qu’il
y a quatre points à l’intérieur de l’intervalle [a,b]
et non deux pour lesquels f prend la même valeur. D’où
contradiction.
Prenons un point $c \in [a,b]$.
Toujours d’après le théorème des valeurs intermédiaires,
$f$ qui est continue prend toutes les valeurs entre $f(a)$ et
$f(c)$ sur $[a,c]$ mais aussi sur $[c,b]$. Pour $x < a$ ou
pour $x > b$, on ne peut pas avoir $f(x) > f(a)$. Sinon
il en résulterait que $f$ prendrait ces valeurs une
troisième fois sur $[x,a]$ ou sur $[b,x]$. On a donc $f(x) <
f(a)$ pour $x$ en dehors de l’intervalle $[a,b]$.
Par conséquent la fonction $f$
est bornée supérieurement sur $\mathbb{ R}$. Soit Max la valeur maximale. Si
cette valeur maximale est prise une fois et une seule, on est
en contradiction avec l’hypothèse initiale. La valeur Max
est alors prise deux fois. D’où
la configuration ci-dessous dans laquelle on constate qu’il
y a quatre points à l’intérieur de l’intervalle [a,b]
et non deux pour lesquels f prend la même valeur. D’où
contradiction.
Nota :
la démonstration est rigoureusement la même si $f(x) <
f(a)$ sur $[a,b]$ avec une valeur minimale Min prise par $f$
sur $\mathbb{ R}$.''
Solution à la partie (b). Nos
correspondants nous ont envoyé
plusieurs exemples.
Type 1.
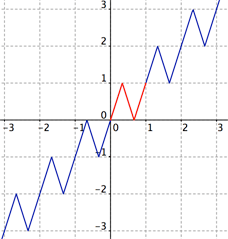
|
La
fonction $f$ représentée ci-contre est définie par :
Pour tout entier $k$
$$\small f(x)
= \left\{
\begin{array}{lcc}
3(x-k) + k & 0
\le x-k \le \frac13 \\
-3(x-k)+2+k & \frac13 \le
x-k \le \frac23 \\
3(x-k) -2+k & \frac23 \le x-k
\le 1
\end{array}
\right ..$$
|
Figure 1: f(x)
La Figure 1 est une légère modification du fichier GeoGebra que nous a envoyé Humbert. Comme son nom l'indique, GeoGebra
combine l'algègre et
les graphiques. On peut le télécharger gratuitement, mais
ça peut prendre un bout de temps pour apprendre à s'en
servir.
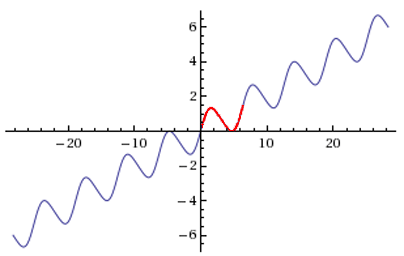
Figure
2: $g(x) = \frac2{3\pi}x + \sin x +\frac1{3\pi}\sin 2\pi$
La Figure 2 est une copie de la page
WolframAlpha produite LoPresti en entrant la commande
graph[2/(3pi)*x + sin(x)
+ 1/(3pi)*sin(2x)]
dans l'espace prévu
à cette fin à la page www.wolframalpha.com.
Vous pouvez explorer la figure en déplaçant
la souris, et modifier l'équation.
D'autres
exemples sont disponibles sur notre page anglaise.
Commentaires. Plusieurs de
nos correspondants ont noté
que plus généralement, il existe une fonction continue qui
prend toutes les valeurs de son image exactement $n$ fois si
et seulement si $n$ est impair. Nous reproduisons ici
l'argument de Humbert.
Fonction
double-image ou 2n-image :
Soit $n$ un entier
strictement positif.
Supposons qu'il existe
une fonction $f$ prenant chacune de ses valeurs $2n$ fois
exactement.
Soit $v$, l'une de ces
valeurs, et $a_1, \ldots, a_{2n}$ ses antécédents par $f$.
Posons $g: x \rightarrow
f(x)-v$.
-
La
fonction $f$ ne peut admettre d'extremum global : celui-ci
devrait, par hypothèse, être atteint $2n$ fois, et on
trouverait alors (à l'aide du théorème des valeurs
intermédiaires) une valeur voisine atteinte au moins $4n$
fois par $f$.
-
$g$ doit être de
signes opposés sur $]-\infty; a_1[$ et sur $]a_{2n};
+\infty[$, sans quoi, étant continue sur le segment qui les
sépare, elle admettrait un extremum global, et $f$ aussi.
-
Parmi les $2n-1$
intervalles bornés découpés sur $\mathbb{
R}$ par $a_1, \ldots, a_{2n}$, il y en a
nécessairement au moins $n$ sur lesquels $g$ prend le même
signe, et il existe une valeur prise au moins deux fois par
$g$ sur chacun de ces $n$ intervalles bornés, plus une fois
sur l'un des deux intervalles non bornés, soit au moins
$2n+1$ fois en tout. $f$ prend donc $2n+1$ fois au moins la
même valeur. Contradiction !
Il
n'existe pas de fonction réelle continue prenant chacune de
ses valeurs 2n fois.
Fonction
triple-image ou 2n+1-image
:
Pour tout entier
strictement positif $n$, la fonction $g_n$ définie
ci-dessous est régulière et atteint chaque réel $2n+1$
fois :
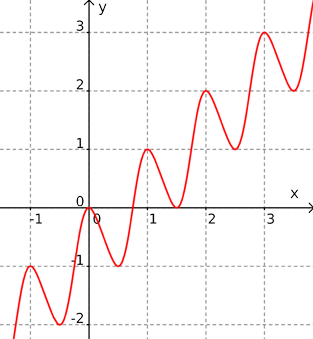
$$g_n:
x \rightarrow x - \frac{1}{4\pi}\sin(4\pi x) +
(2n+1)\frac{cos(2\pi x) – 1}{4}.$$
|

