|
Solution au problème d'avril 2010
| Le problème: |
 |
MP95
Problème d'avril 2010
Que
peut-on dire au sujet des angles d'un triangle dont la somme des cubes des
côtés divisé par son périmètre donne l'aire du carré sur un
de ses côtés?
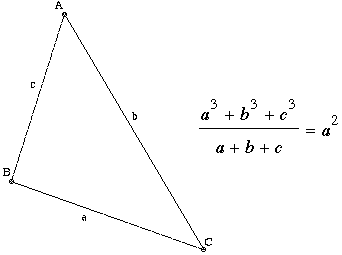
Notre problème provient d'une liste de problèmes
suggérés par Murray Klamkin pour l'Olympiade Mathématique
Canadienne de 1983. Nous avons reçu des solutions
correctes de
Bahman Ahmadi
(Regina) |
Sébastien Dumortier
(France) |
Farid Alberto Lian Martínez
(Colombie) |
Halima Bashier
(Regina) |
Amit Elazari |
Remo Mantovanelli
(Italie) |
Bojan Basic
(Serbie) |
Mei-Hui Fang
(Autriche) |
Milan Pavic
(Serbie) |
Luigi Bernardini
(Italie) |
Constantin Fishkin
(Ontario) |
Arnaud Piquerez
(France) |
José Borges
(Portugal) |
Philippe Fondanaiche
(France) |
John T. Robinson
(États Unis) |
Bernard Carpentier
(France) |
Bruce Golfman
(Autriche) |
Albert Stadler
(Suisse) |
Bernard Collignon
(France) |
Cornel Gruian
(Roumanie) |
A. Teitelman
(Israël) |
Andrew Cooke
(Chine) |
Benoît Humbert
(France) |
Jan van Delden
(Pays-Bas) |
Shai Covo
(Israël) |
Magnus Jakobsson
(Suède) |
Ray Van Raamsdonk
(Colombie Britannique) |
Dan Dima
(Roumanie) |
Wolfgang Kais
(Allemagne) |
Benjamin Louradour
(France) |
Allen Druze
(États Unis) |
Normand LaLiberté
(Ontario) |
 KURIHARA Tomohiro KURIHARA Tomohiro
(Japon)
|
|
La solution:
Nous allons démontrer que lorsque ΔABC est étiquetté de
telle sorte que l'angle à A est opposé au
côté dont on prend le carré, alors ∠A =
60°. Les mesures des deux autres angles peuvent peuvent être
n'importe quelle paire de valeurs dont la somme est 120°.
À
partir du quotient donné, on obtient
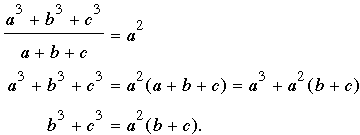
Puisque b3 + c3 = (b2 - bc + c2)(b + c) et b + c > 0
(les longueurs de côtés d'un triangle étant
positives par définition), la dernière équation se
simplifie ainsi
b2 - bc + c2 = a2.
Selon la loi du cosinus, a2 = b2 + c2 - 2bc cos A. En comparant les deux two expressions pour a2, on obtient – bc = –2bc cos A, soit
cos A = 1/2.
Puisque les mesures des angles d'un
triangle sont entre 0° et 180°, on a bien ∠A =
60°, qu'il fallait démontrer. Réciproquement,
puisque toutes les étapes sont récersibles, si ∠A = 60°, alors 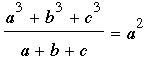 . .
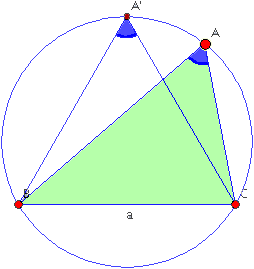
Le triangle A'BC dans la figure
ci-haut est équilateral. En cliquant sur la figure vous
ferez apparaître un applet où le sommet A peut être
déplacé sur l'arc de cercle entre B et C.
Vous pouves alors générer tous les triangles avec la
propriété en question, qui ont a = BC comme côté. La valeur de l'angle à A est
toujours 60° (Proposition 20 du troisième livre d'Euclide)
bien que les angles à B et C varient. De même, les longueurs des côtés b et c sont variable, mais selon la loi
du cosinus, b2 + c2 - 2bc cos A et 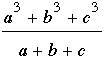 sont
constants, égaux à a2. sont
constants, égaux à a2.
|

