Solution au problème de septembre 2008

Le problème:

Dans le film Gunsmoke: The Last Apache, on trouve une variante intéressante de la roulette russe: On pose six verres de whisky sur le bar, mais un d'entre eux contient une dose mortelle de strychnine. Tour à tour le héros et le vaurien vident les verres. Le héros commence, et bien sûr il gagne. Au vaurien qui agonise, il dit: "Ha, tu aurais du commencer, le premier joueur a de meilleures chances!" Notre question du mois: Que pensez-vous des aptitudes mathématiques du scénariste? Plus généralement, dans un duel avec n verres dont un seul contient un poison, que deux participants vident tour à tour jusqu'à ce qu'un d'entre eux s'empoisonne, quelle est la probabilité que ce soit le premier qui perde?

La solution:

Nous avons reçu des solutions correctes de

     Tous nos correspondants s'entendent pour dire que le scénariste est dans les patates: Le jeu est équitable, chacun des participants a une chance sur deux de gagner. On peut s'en convaincre en imaginant que le duel se déroule de la façon suivante: chacun des participants reçoit trois des six verres à l'avance; et comme la strychnine se trouve de façon équiprobable dans chacun des six verres, la probabilité de trouver le poison dans un de ses verres est de trois sur six pour chacun des participants.  On peut également résoudre le problème avec un arbre de probabilités:

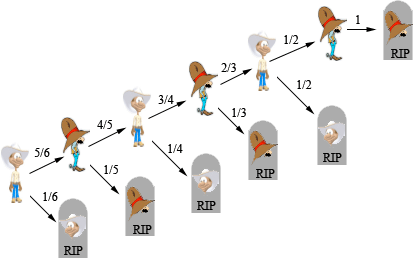
Le diagramme indique que

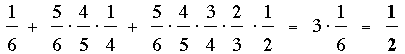
Presque tout le monde a remarqué que le problème est tout aussi facile avec k verres dont un seul contient de la strychnine. Comme le dit Bernard Carpentier,

"Au lieu de boire les verres un à un à tour de rôle, imaginons que les 2 personnages H et V choisissent à tour de rôle les verres qu'ils vont boire et les installent devant eux avant de les boire selon la règle du jeu fixée.

nombre de verres pair k = 2n (2n-1 B et 1M)

H tire en premier. Donc H aura un lot de n verres et V aussi. Le mauvais verre a donc n chances sur 2n de se trouver dans le lot de H et autant de chances de se trouver dans le lot de V. La probabilité pour que H meure sera de n/2n = 1/2.

nombre de verres impair k = 2n+1 (2n B et 1M)

H tire en premier. Donc H aura un lot de n+1 verres et V de n verres. Le mauvais verre a donc n+1 chances sur 2n+1 de se trouver dans le lot de H et seulement n chances sur 2n+1 de se trouver dans le lot de V. La probabilité pour que H meure sera de (n+1)/(2n+1) = (n+1/2+1/2)/ (2n+1) = 1/2 +1/2k.

Moralité

Tirer en premier

- est indifférent si le nombre k de verres est pair (la probabilité de mourir étant 1/2 ),

- est défavorable si le nombre k de verres est impair (la probabilité de mourir étant 1/2 + 1/2k).''

Une variante supplémentaire est considérée dans "Whisky, Marbles, and Potholes", par J. Chris Fisher et Denis Hanson, Mathematics Magazine, 68:1 (février 1995), pages 50-54. On y traite le cas où r des k verres contiennent du poison. Il est possible de donner une formule donnant la probabilité que le héros s'empoisonne, bien que ce ne soit pas si facile.