Solution au problème d novembre 2008

Le problème:
	Pour quels entiers k ≥ 3 la valeur 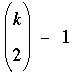est-elle une puissance de premier, c'est à dire un nombre de la forme pn où p est premier?

La solution:

Nous avons reçu des solutions correctes de

     Notre problème de novembre est le problème 984 de Crux Math, 12:1 (janvier 1986), pages 15-16.

Solution. k peut prendre les valeurs 3, 4, 5 et 8. Nous reproduisons ici la solution de Catherine-A Nadault.

"Si on pose k = s – 1 , le nombre étudié s'écrit : N = s(s – 3)/2 (avec s ≥ 4).

1. supposons s de la forme s = 2m (avec m ≥ 2), alors N = m(2m – 3) et :
   
   * m = 2 convient : s = 4 , k = 3 et N = 2 = 2¹.
   
   ** si m > 2 : m et (2m – 3) sont tous deux plus grands que 1 , donc si N est une puissance du nombre premier p , celui-ci divise m et (2m – 3) donc il divise 3.
   
   Dès lors p = 3 et, en supposant  m = 3^q (avec q ≥ 1), il vient : N = 3^q×3×[2×3^q-1 – 1].
   
   Il en résulte que le facteur [2×3^q-1 – 1] doit aussi être une puissance de 3 , ce qui n'est possible que si q = 1 : en effet, si q > 1 , [2×3^q-1 – 1] ne peut être divisible par 3 , puisque 2×3^q-1 l'est et, à l'inverse, si q = 1 on a : 2×3^q-1 – 1 = 1 = 3⁰ .
   
   On a alors : q = 1 , m = 3 , s = 6 , k = 5 et N = 9 .
   
   
2. supposons s de la forme s = 2m + 1 (avec m ≥ 2), alors N = (2m + 1)(m – 1) et :
   
   * m = 2 convient : s = 5 , k = 4 et N = 5 = 5¹.
   
   ** si m > 2 : (2m + 1) et (m – 1) sont tous deux plus grands que 1 , donc si N est une puissance du nombre premier p , celui-ci divise (2m + 1) et (m – 1) donc il divise [(2m + 1) – 2*(m – 1)] = 3.
   
   Dès lors p = 3 et, en supposant (m – 1) = 3^q (avec q ≥ 1), il vient : N = 3^q×3×[2×3^q-1 + 1].
   
   Le raisonnement précédent montre que le facteur [2×3^q-1 + 1] doit être une puissance de 3 et que ceci n'est possible que lorsque q = 1 ... Il en résulte que l'on a alors : q = 1 , m = 3¹ + 1 = 4 , s = 9 , k = 8 et N = 27 = 3³.
   
   En résumé : les seules valeurs de k qui conviennent sont k = 3 , 4 , 5 et 8.''