|
Solution au problème de mai 2009
| Le problème: |
 |
MP87 mai 2009
Il y a quelque chose qui cloche dans
l'ordre habituel des entiers qu'on
nous apprend dès l'enfance. En effet, lorsqu'on compte 1, 2, 3,
..., on
note que la somme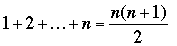 des
n premiers entiers positifs n'est pas toujours un multiple de n.
Lorsque n est impair ça va, mais par contre 1 + 2 n'est pas un
multiple
de 2, 1 + 2 + 3 + 4 n'est pas un multiple de 4, et ainsi de suite.
Aussi, notre problème de ce mois est de trouver une meilleure
façon
d'ordonner les entiers positifs: des
n premiers entiers positifs n'est pas toujours un multiple de n.
Lorsque n est impair ça va, mais par contre 1 + 2 n'est pas un
multiple
de 2, 1 + 2 + 3 + 4 n'est pas un multiple de 4, et ainsi de suite.
Aussi, notre problème de ce mois est de trouver une meilleure
façon
d'ordonner les entiers positifs:
Trouver une suite a1, a2, a3, ...
d'entiers positifs telle que
(i)
tout entier positif apparait une et une seule fois dans la suite, et
(ii)
pour tout n, a1 + a2 + ... + an est un
multiple de an
Nous avons reçu des solutions correctes de
Philippe Fondanaiche (France) |
John T. Robinson (États-Unis) |
Patrick J. LoPresti (États-Unis) |
Albert Stadler (Suisse) |
|
La solution:
Notre solution combine des idées de tous nos
correspondants. Nous ne pouvons commencer avec a1 =
1, parce qu'il n'y aurait alors aucune façon de choisir a2 en respectant la condition (ii). Posons plutôt a1 =
2, et utilisons la stratégie suivante:
Stratégie 1:
Si a1, a2, ..., an sont déjà choisis, posons sn = a1 + a2 + ... + an,
et choisissons pour an+1 le plus petit diviseur de sn qui
n'est pas encore choisi.
n:
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
an:
|
2
|
1
|
3
|
6
|
4
|
8
|
12
|
9
|
5
|
10
|
15
|
25
|
20
|
24
|
16
|
sn:
|
2
|
3
|
6
|
12
|
16
|
24
|
36
|
45
|
50
|
60
|
75
|
100
|
120
|
144
|
160
|
Les premières valeurs de an sont données dans la table ci-haut. Pour n > 1 nous avons sn > a1, a2, ..., an, donc il existe toujours un choix possible pour an+1,
soit sn (au pire). Clairement, une suite construite de telle manière
respecte la condition (ii), mais la condition (i) pose problème.
Nos correspondants ont repéré cette suite dans l'Encyclopédie
en ligne des suites de nombres entiers http://www.research.att.com/~njas/sequences/index.html?language=french,
où il est conjecturé que cette suite contient tous les
nombres entiers. A moins de démontrer la conjecture, il est donc
impossible de poursuivre indéfiniment avec la Stratégie 1.
Stratégie 2:
Si a1, a2, ..., an sont déjà choisis, et l'entier N tarde à paraître, au
point d'en inquiéter certains. Alors nous nous assurons d'abord
d'avoir une somme sn qui n'est pas une puissance de 2, quitte à utiliser la Stratégie
1 pour une étape supplémentaire si besoin est. Ensuite,
nous commençons à donner aux nouveaux termes la forme ak+1 = sk
jusqu'à ce qu'il soit possible d'atteindre un multiple de N en ajoutant des puissances de 2.
La première étape est donc de s'occuper de
la situation particulière où sn = 2k.
Notons qu'alors, il doit exister une puissance de 2 inférieure
à 2k qui n'est pas utilisée, car autrement nous aurions
sn - 1 = 1 + 2 + ... + 2k-1 < a1 + ... + an = sn,
qui impliquerait n = k+1 et un deuxième
terme égal à 1, contradiction. Par conséquent, la
Stratégie 1 donne un nouveau terme 2i tel que i < k, et la somme suivante 2k + 2i n'est pas une
puissance de 2.
Nous pouvons donc supposer que sn n'est pas une
puissance de 2, et nous nous appliquons à étendre la
suite pour pouvoir y insérer N. Nous posons an+1 = sn donc sn+1 = 2sn, puis an+2 = 2sn et sn+2 = 4sn,
et nous continuons à donner aux nouveaux termes la forme an+j = 2j-1sn pour obtenir to sn+j = 2jsn, jusqu'à ce que 2j soit assez grand. Pour clarifier le sens que nous donnons à
``assez grand'', nous examinerons la suite des puissances de 2 modulo N.
Pour tout entier i,
notons bi le reste
de la division de 2i par N. Puisqu'il n'existe
qu'un nombre fini de restes possibles, il existe deux entiers i, k tels que bi+k = bi. Nous avons bi+k+1 = bi+1, bi+k+2 = bi+2, et la suite
continue indéfiniment à faire le tour des termes bi, bi+1, ...,bi+k-1. Nous avons alors bi + bi+1 + ... + bi+k-1 ≡ 0 (mod N), puisqu'avec t = bi + bi+1 + ... + bi+k-1, nous obtenons
2 t = 2 bi + 2bi+1 + ... + 2bi+k-1 ≡ bi+1 + bi+2 + ... + bi ≡ t (mod N)
donc t ≡ 0 (mod N).
Par ailleurs, sn peut être représenté comme somme de puissances
distinctes de 2, donc pour tout j > i, 2 jsn est
congru modulo N à une
somme de termes parmi bi, bi+1, ...,bi+k-1.
L'identité 2 bm ≡ bm+1 (mod N) permet de simplifier
la somme jusqu'à l'obtention d'une somme de termes distincts
parmi bi, bi+1, ..., bi+k-1 qui est congrue
modulo N à 2 jsn. Notons bm(1), ..., bm(r) les termes parmi bi, bi+1, ..., bi+k-1 qui ne sont pas
utilisés dans cette somme. Si j est assez grand, nous pouvons choisir une suite décroissante 2 j > 2 e(1) > ... > 2 e(r) telle que 2 e(p) ≡ bm(p) (mod N), et 2 e(1),
..., 2 e(r) n'apparaissent pas dans la suite a1, a2, ..., an.
Puisque sn n'est
pas une puissance de 2, 2e(1),
..., 2e(r) ne font
pas partie des termes suivants an+1 = sn,
..., an+j = 2 j-1sn.
Donc nous pouvons poser an+j+1 = 2 e(1) , sn+j+1 = 2 e(2)q1, an+j+2 = 2 e(2) , sn+j+1 = 2e(3)q2, ...,
jusqu'à an+j+r =
2 e(r). Nous avons alors
sn+j+r = 2jsn + 2e(1) + ... + 2e(r) ≡
0 (mod N).
Nous pouvons donc choisir an+j+r+1 = N.
|

