|
Solution au problème de janvier 2009
| Le problème: |
 |
Soit a0 = 2009 et 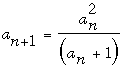 pour tout entier non-négatif n. Demontrer que lorsque 0 ≤ n ≤ 1005, 2009 – n est le plus grand entier plus petit ou égal à an. pour tout entier non-négatif n. Demontrer que lorsque 0 ≤ n ≤ 1005, 2009 – n est le plus grand entier plus petit ou égal à an.
|
La solution:
Solution. Notre problème du mois est une version modifiée d'un problème de la liste courte A1 proposé pour la 35th International Mathematical Olympiad (Hong Kong, 1994). Nous avons reçu des solutions correctes de
Bojan Basic (Serbie) |
Seb Lebre (?) |
Luigi Bernardini (Italie) |
Matthew Lim (États-Unis) |
Lou Cairoli (États-Unis) |
Jeff Lindstrom (Ontario) |
Bernard Carpentier (France) |
Catherine Nadault (France) |
Bernard Collignon (France) |
Shpetim Rexhepi (Macédoine) |
Olivier Cyr (France) |
John T. Robinson (États-Unis) |
Philippe Fondanaiche (France) |
Heri Setiyawan (Indonésie) |
Cornel Gruian (Roumanie) |
Albert Stadler (Suisse) |
Omran Kouba (Syrie) |
|
Solution.
Nous reproduisons ici la solution de Bernard Collignon
Le résultat est évidemment vrai pour n = 0, car a0 = 2009 = 2009 – 0,
donc il suffit de vérifier par la suite que le résultat est vrai pour tout entier n tel que 0 < n
≤ 1005.
Pour tout entier positif n, an > 0 , résultat facilement démontré par récurrence sur n.
Donc la suite est bien définie pour tout entier naturel n puisque 1 + an > 1 et donc 1 + an ≠ 0.
Pour tout n :
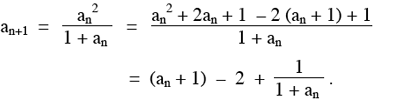
Donc : an+1 = an – 1 + 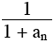 ( E ) avec 0 < ( E ) avec 0 < 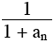 < 1 puisque an > 0. < 1 puisque an > 0.
Pour tout entier n > 0 on a de proche en proche à partir de l’égalité ( E ) :
a1 = a0 – 1 + 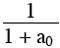 ( 1 ) ( 1 )
a2 = a1 – 1 + 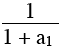 ( 2 ) ( 2 )
a3 = a2 – 1 + 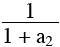 ( 3 ) ( 3 )
ETC ….
an = an – 1 – 1 + 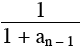 ( n ) ( n )
En additionnant membre à membre ces n égalités et en simplifiant on obtient pour tout n > 0 :
an = a0 – n + 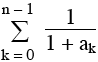 , c'est-à-dire : an = 2009 – n + , c'est-à-dire : an = 2009 – n + 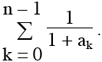 . .
Il suffit de montrer que l’on a pour tout n tel que 0 < n 1005, 0 ≤ Rn = 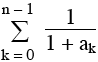 < 1 . < 1 .
La suite ( Rn ) étant strictement positive et croissante, puisque 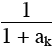 > 0 pour tout entier positif k, il suffit en fait de montrer que l’on a pour n = 1005 : > 0 pour tout entier positif k, il suffit en fait de montrer que l’on a pour n = 1005 :
R1005 = 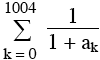 < 1 . < 1 .
Or pour tout 1 ≤ k ≤ 1005 , ak = 2009 – k + 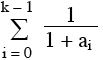 > 2009 – k , > 2009 – k ,
car pour tout i : 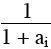 > 0. > 0.
D’où pour tout 0 ≤ k ≤ 1005 :
1 + ak > 2010 –k 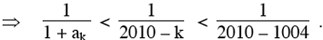
Pour tout 0 < k 1005 : 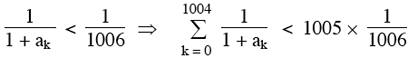 . .
Bilan : R1005 < 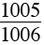 et donc on a bien 0 < R1 < R2 < …….. < R1005 < 1 . et donc on a bien 0 < R1 < R2 < …….. < R1005 < 1 .
Plusieurs correspondants ont noté que 2009 - n est la partie entière de an pour des valeurs de an supérieures à 1005. Nous reproduisons ici la solution de Nadault qui démontre que cette identité est valide jusqu'à n = 1271.
|

