|
Solution au problème de avril 2009
| Le problème: |
 |
Trouver deux entiers a et b tels
que ni 7, ni 18 ne divise ab(a+b), alors que 77 divise (a+b)7-a7-b7.
|
La solution:
Nous avons reçu des solutions correctes de
Bojan Basic (Serbie) |
Tarik Kaced (France) |
Ruban Victor Cohen (Argentine) |
Omran Kouba (Syrie) |
Bernard Collignon (France) |
Matthew Lim (États-Unis) |
Allen Druze (États-Unis) |
Benjamin Louradour (France) |
Sébastien Dumortier (France) |
Pavan Manjunath (Inde) |
Philippe Fondanaiche (France) |
John T. Robinson (États-Unis) |
Cornel Gruian (Roumanie) |
Albert Stadler (Suisse) |
| Edward Doolittle (Regina) |
|
Notre problème d'avril s'inspirait du
problème 2 de la 25ème Olympiade Mathématique
Internationale (Prague, 1984). On trouve l'énoncé
original et la solution de Jeremy Kahn dans International
Mathematical Olympiads 1978-1985, édité par Murray
S. Klamkin (Mathematical Association of America, New
Mathematical Library #31, 1986). La pluspart de nos
correspondants nous ont donné une solution
générale, mais Doolittle, Kouba, Lim, et Robinson sont
allés plus loin et ont trouvé des relations
nécessaires et suffisantes entre les entiers a et b:
- 77 divise (a + b)7 – a7– b7 mais ni 7 ni 18 ne
divise ab(a + b) est équivalent à
- b = 18a + 343k, où a et k sont des entiers tels que 7 ne
divise pas a et 9 ne divise pas ak(a + k);
ou bien cette condition est valide lorsque les rôles de a et b sont interchangés.
|
Notre démonstration combine leurs arguments.
Examinons d'abord quelques exemples. Lorsque a = 1; alors k = 0 n'est pas permis (puisque 9 divise 0), mais k = 1 donne b = 361, et k = –1 donne b = –325. Dans ces deux
exemples, le quotient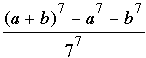 est plutôt
grand; on obtient un quotient plus raisonnable lorsque a = 20
et k = –1; on a alors b = 17 et est plutôt
grand; on obtient un quotient plus raisonnable lorsque a = 20
et k = –1; on a alors b = 17 et 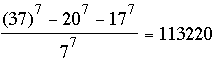 . .
Démonstration.
En factorisant, on obtient
(a + b)7 – a7– b7 = 7ab(a
+ b)(a2 + ab + b2)2.
Ainsi (a + b)7 – a7– b7 est un multiple de 77 lorsque ab(a + b)(a2 + ab + b2)2 est un multiple de 76.
Et puisque 7 ne divise pas ab(a + b), 76 doit diviser (a2 + ab + b2)2 et ainsi,
73 divise a2 + ab + b2.
Notons que 18 × 19 = 342 = 73 – 1. La
magie de l'arithmétique modulaire permet de factoriser
l'expression quadratique modulo 73 comme suit
a2 + ab + b2 ≡ a2 + ab + (1 – 343)b2
≡ (a + 19b)(a – 18b) ≡
–19(18a – b)(a – 18b) ≡ 0 (mod 73).
(En d'autres termes, 73 divise –19(18a – b)(a – 18b), et divise donc (18a – b)(a – 18b).) Or 7 ne peut diviser
à la fois 18a – b et a – 18b,
car alors la différence 18a – b – (a – 18b)= 17(a + b) serait un multiple de 7, donc a + b serait un multiple de 7, ce qui contredit la condition
selon laquelle 7 ne divise ab(a + b). Par
conséquent, 73 divise soit 18a – b,
soit a – 18b, mais pas les deux. Par
symétrie, on peut supposer que 73 = 343 divise 18a – b. Notons b = 18a + 343k. Alors la condition stipulant que
7 ne divise pas ab(a + b) = a(18a + 343k)(19a + 343k) ≡ 6a (mod 7) se réduit à
7 ne divise pas a.
Examinons la deuxième condition, selon la quelle 18 ne divise
pas ab(a + b). Puisque le produit est
nécéssairement pair, celle-si se réduit à 9
ne divise pas ab(a + b). Avec b = 18a + 343k ≡ k (mod
9), on a
ab(a + b) ≡ ak(a + k) (mod 9),
donc 18 divise ab(a + b) si et
seulement si 9 divise ak(a + k), ce qui
complète la démonstration.
D'autres commentaires sont disponibles sur notre page
anglaise.
|

