|
Solution au problème d'été 2008
| Le problème: |
 |
l'été 2008
Pour l'été, le Problème du Mois vous offre sa version de la suite d'un conte bien connu.
La lecture du testament permit aux sept frères de se revoir et de se rappeler leur enfance. De bons souvenirs, bien sûr, mais aussi de mauvais souvenirs, des histoires
terribles. Une année de grande famine, leurs parents les avaient conduits dans la forêt pour les perdre, et ils avaient retrouvé leur chemin seulement grâce aux cailloux que le plus jeune d'entre eux avait semés en chemin. Une autre fois, ils avaient dû se sauver d'un ogre qui les poursuivait avec des bottes de sept lieues.
Maintenant, leurs parents étaient décédés, leur léguant bien sûr leur bonne vieille maison dans les bois. Mais, chose surprenante, le testament révélait aussi que dans la cave, ils trouveraient un coffre verrouillé dont la clef se trouvait sous le seau à charbon. Dans le coffre se trouvait le trésor que leurs parents avaient gardé pour eux.
Les sept frères filèrent donc à la cave de la vieille maison. Lorsqu'ils soulevèrent le seau à charbon, un déclic se fit entendre, puis un bruit d'engrenage, et une porte se referma derrière eux. C'était une lourde porte avec une étrange serrure à combinaison, constituée de neuf roulettes numérotées disposées en carré trois par trois. Ils étaient prisonniers dans la cave. Par contre, la clef était bien sous le seau à charbon. Le coffre s'ouvrit en grincant, un rat en sortit, et les sept frères découvrirent qu'il ne contenait rien qu'une lettre et un vieux bout de papier rongé par le rat. La lettre était le dernier message de leurs parents:

Les frères se précipitèrent vers le coffre pour en retirer le bout de papier. Avec horreur ils découvrirent que le rat avait grignoté le coin du bas à gauche du puzzle dont dépendait leur survie.
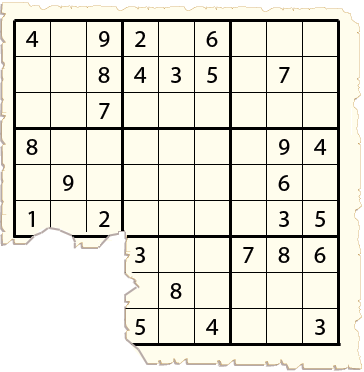
Fort heureusement, ils étaient tous très fort en sudoku, et réussissaient le puzzle du journal tous les dimanches. Ils copièrent donc le puzzle en sept exemplaires, en se disant qu'au moins un d'entre eux arriverait à le résoudre malgré le coin manquant. Le plus jeune était habituellement le plus vif, mais en cette occasion il se révéla étrangement méditatif, inscrivant quelques chiffres puis s'interrompant pour de longues réflexions, alors que ses frères scribouillaient comme des damnés.
Quelques minutes plus tard, les six posèrent leur plume en s'écriant "je l'ai!''. Mais en comparant leurs solutions ils s'aperçurent qu'elles étaient toutes différentes. Chacune avait les chiffres 1 à 9 apparaissant une et une seule fois dans chaque ligne, chaque colonne et chaque carré 3 par 3, mais l'apétit du rat ayant complètement détruit le coin du bas à gauche, il était impossible de dire laquelle de leurs solutions était la bonne. "Bon, ça y est'' se dirent-ils," nous sommes cuits'' et ils éclatèrent en sanglots.
Un peu plus tard, au millieu des pleurs et des cris, une petite voix s'écria soudain "je l'ai''. C'était le plus jeune, que ses six frères avaient oublié. Sa solution était différente de toutes les leurs, mais il affirmait que c'était la bonne. Que faire? C'était le plus jeune, le plus brillant, ils s'étaient maintes fois fiés à son jugement et c'est d'ailleurs ce qui leur avait permis de survivre à leur enfance. Ils réglèrent donc les roulettes de la serrure selon le carré central de la solution de leur petit frère, tirèrent la poignée et ···
Chers lecteurs, nous interrompons ici notre récit, et nous vous souhaitons un bon été. Nous publierons la fin en septembre. Si vous devinez la fin, vous pouvez nous l'envoyer au Problème du Mois, avec une justification complète.
|
La solution:
. . . La porte s’ouvrit et les sept frères déguerpirent hors de la cave, hors de
la maison, à travers les bois vers une clairière où ils plongèrent à l’instant où la
maison explosait derrière eux. Ils s’étaient échappés de justesse. Lorsqu’ils eurent récupéré leur souffle, ils remarquèrent qu’ils avaient tous gardé le bout de papier sur lequel chacun avaient noté sa solution au puzzle sudoku. Ils savaient maintenant que seulement le plus jeune avait su trouver la bonne, et lui demandèrent comment il avait fait. Voici ce qu’il répondit: "Avant que le rat mange le carré du bas à gauche, le puzzle a dû ressembler à quelque chose comme çà:
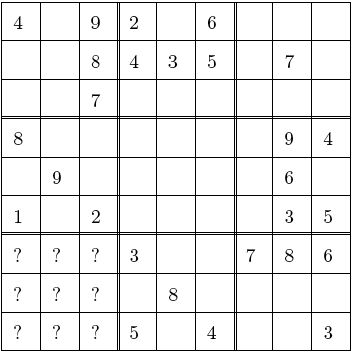
Certains des points d’interrogation correspondent à des cellules vides, et d’autres
à des chiffres donnés dans le puzzle original, qui rendaient la solution unique.
Lorsque cette information est disparue, le puzzle est devenu plus facile à résoudre
en quelque sorte. Le défiétait de retrouver la solution du puzzle original plutôt
qu’une des multiples solutions du nouveau puzzle. J’ai dû me retenir de placer
des numéros dans les cellules juste parce que ça marche, et me restreindre aux
numéros qui étaient forcés dans une cellule pour une des raisons suivantes:
- Tous les autres numéros apparaissent ailleurs dans la même ligne, la même
colonne ou le même carré trois par trois.
- Ce numéro ne peut apparaître ailleurs dans la même ligne, la même colonne
ou le même carré trois par trois.
En suivant ces règles, j’ai pu remplir la grille partiellement, comme suit:
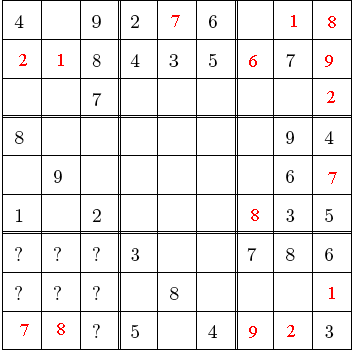
Toutes vos solutions coïncident avec la mienne jusqu’à ce point. Mais à partir de
là j’étais bloqué. Si j’avais pu me servir du coin inférieur gauche, j’aurais sans
doute pu continuer de la même manière, comme j’en ai l’habitude, et trouver
l’unique solution. Mais, dans ce cas, j’aurais non seulement trouvé la solution
dont nous avions besoin, mais en plus démontré que cette solution est la
seule solution au puzzle original. C’était plus que ce dont nous avions besoin.
Était-il possible d’en faire moins et de quand même trouver la solution du puzzle
original? Je me suis alors rendu compte du fait que je pouvais utiliser l’unicité
de la solution comme hypothèse plutôt que la démontrer:
Au haut à droite, seulement le 3, le 4 et le 5 manquent, et au bas à droite,
seulement le 4 et le 5 manquent. Le 3 du haut va dans la septième colonne, à
la ligne 1 ou 3. On peut placer le 3 à la ligne 1 sans contradiction apparente.
En fait, une de vos solutions a le 3 à cette position. Mais dans ce cas, les 4 et
5 des lignes 3 et 8 vont dans les colonnes 7 et 8, dans un certain ordre, et on
obtient une deuxième solution en les interchangeant. Or, c’est impossible
puisque le puzzle original avait une solution unique. Donc, le carré original du
bas à gauche contenait de l’information qui servait à bloquer cette solution, et
le 3 de la septième colonne va à la ligne 3.
Ce placement m’a permis de remplir la grille un peu plus, en plaçant le 3
du carré du haut à gauche puis en complétant les carrés du haut et du bas à
droite. Le puzzle était alors comme suit.
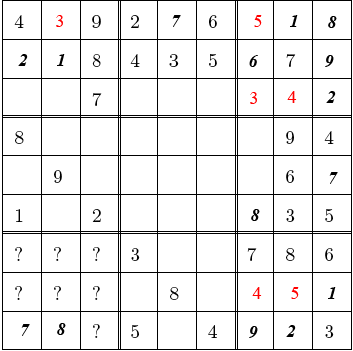
Je me suis alors concentré sur le carré du haut à gauche, auquel il ne manquait
que le 5 et le 6. Encore une fois, on n’aboutit à aucune contradiction en
plaçant le 5 dans la deuxième colonne, sauf qu’on obtient une deuxième solution
en interchangeant les 3 et 5 des carrés du haut à gauche et à droite. Comme le
puzzle original a une solution unique, le carré du haut à gauche doit avoir son 5
dans la première colonne. Ceci m’a permis de remplir le puzzle beaucoup plus:
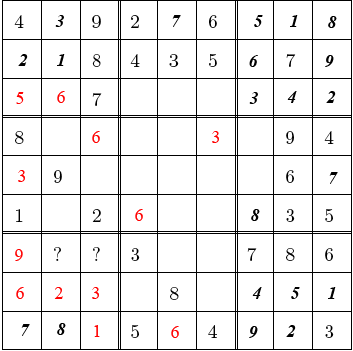
Seulement le 4 et le 5 manquaient au carré du bas à gauche. J’ai facilement
vérifié qu’avec le 4 dans la deuxième colonne et le 5 dans la troisième,
j’aboutissait à de solutions multiples. Donc le 5 allait plutôt dans la deuxième
colonne et le 4 dans le troisième. J’avait alors reconstitué le coin manquant, et
je pouvais compléter le puzzle.”
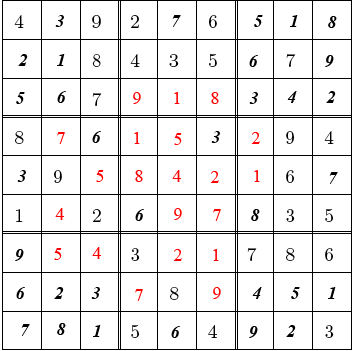
Et voici comment le petit poucet sauva encore une fois sa famille d’un désastre.
Les sept frères retournèrent inspecter les ruines de la maison. Tout avait été
détruit; il ne restait pas un bonnet de nuit, pas une miette de pain et pas même
la moindre plume. Alors ils se saluèrent et repartirent chacun son chemin, avec
leur petit bout de sagesse nouvellement acquise qui vaut vraiment plus que tous
les trésors d’or et d’argent.
Commentaires Dans “Sudoku squares and chromatic polynomials” [Notices
of the Amer. Math. Soc., 54 (2007) no. 6, 708-717], A. Herzberg et R. Murty
font le lien entre les puzzles sudoku et le coloriage de graphes. Notre problème
de l’été est inspiré d’une application de “l’argument de chaînes de Kempe”
aux puzzles sudoku. Kempe se servit de cet argument en 1879 lorsqu’il tenta de
démontrer le problème des quatre couleurs, selon lequel quatre couleurs suffisent
pour colorier les régions d’une carte géographique de telle sorte que les régions
adjacentes aient toujours des couleurs distinctes. Toutefois, la preuve de Kempe
était incomplète, et le problème des quatres couleurs demeura ouvert jusqu’à
l’obtention de démonstrations complètes par Appel et Hacken en 1976 et par
Robertson, Sanders, Seymour et Thomas en 1996.
Notre problème de l’été a été résolu correctement par Philippe Fondanaiche
(France), Minghua Lin (Chine), Jerry Powidajko (Canada), Gérard Billion
(France), Jose Arraiz (Brésil), Jacques Mertzeisen (France), Patrick J. LoPresti
(états-Unis), Zachary Friggstad (Canada) et Bojan Bašić (Serbie). Comme
pour les solutions modernes du problème des quatres couleurs, plusieurs de nos
correspondants se sont servi d’ordinateurs pour montrer que le puzzle a 26 solutions
lorsque le carré du bas à gauche manque. Nous donnons un lien plus bas
au programme C de Friggstad, à la solution de Fondanaiche sans ordinateur,
et à la solution de Lim qui résoud le problème sans ordinateur, puis avec, en
utilisant l’algorithme des “liens X dansants” de Donald Knuth.
|

