Solution au problème de septembre 2007

Le problème:

Six points sont disposés de telle sorte que les longueurs des quinze segments qui les relient deux à deux sont toutes différentes, et qu'aucun segment passe par trois de ces points. Démontrez  qu'un de ces segments est en même temps le plus long côté d'un des triangles formés par les six points, et le plus court côté d'un autre triangle.

Peut-on obtenir la même conclusion à partir de cinq points plutôt que six? 

Nous avons reçu des solutions correctes de Philippe Fondanaiche (France), Wolfgang Kais (Allemagne), John T. Robinson (États-Unis), et K. Sengupta (Inde).  Nos correspondants ont remarqué le rôle que joue le nombre de Ramsey R(3,3) dans notre problème. Une solution élémentaire dans le langage de la théorie de Ramsey peut etre trouvée dans plusieurs livres, et aussi sur les sites
http://www.cut-the-knot.org/Curriculum/Combinatorics/ThreeOrThree.shtml,
et
http://en.wikipedia.org/wiki/Ramsey's_theorem.
qui nous ont été communiqués par John Robinson. Notre version du problème provient de Mathematical Miniatures par Svetoslav Savchev et Titu Andreescu [publié en 2003 par the Mathematical Association of America].

Nous reproduisons ici la solution de Philippe Fondanaiche.

Problème de septembre 2007 Le plus long est en même temps le plus court

On démontre d’abord la propriété (P) suivante : si l’on colorie en bleu ou en rouge les quinze segments qui relient deux à deux six points dont trois quelconques d’entre eux ne sont jamais colinéaires, il y a nécessairement au moins un triangle dont les trois côtés sont de la même couleur. Voir figure n°1 ci-après :

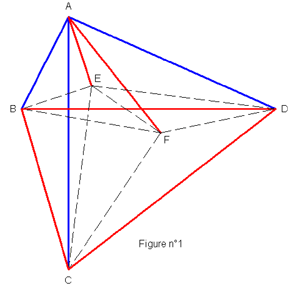
En effet, d’un point donné, A par exemple, il y a au moins trois segments qui sont de la même couleur (bleu par exemple) : AB,AC et AD dans la figure ci-dessus. Dès lors si l’on veut éviter que ABC ou ABD ou ACD soit monocolore (bleu), les segments BC,BD et CD sont tous trois rouges. Mais alors BCD est monocolore (rouge).

Il y a C(6,3) = 20 triangles dont les sommets sont choisis parmi les six points A,B,C,D,E et F. Dans chacun de ces triangles, on identifie par un trait noir le plus grand côté. Comme les quinze distances qui séparent les points sont toutes différentes, il est unique. On dispose ainsi d’un coloriage à deux couleurs avec les côtés en trait noir qui ont la propriété d’être au moins une fois les plus grands côtés de triangles et les côtés en trait vert qui n’ont pas cette propriété. Il existe au moins deux segments verts qui sont les deux plus petits segments parmi les quinze. Voir figure n°2 ci-après :

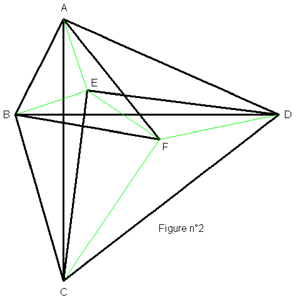
D’après la propriété (P), il y a au moins un triangle monocolore parmi les vingt triangles. A priori, il peut être noir ou vert. Il ne peut pas être vert, car le plus grand côté de ce triangle serait noir. D’où contradiction. Le triangle monocolore est donc noir. Le plus petit côté de ce triangle est alors le plus grand côté d’un triangle adjacent.

Que se passe-t-il avec cinq points ?

La propriété (P) n’est plus vraie et on peut colorier les C(5,2) = 10 segments en bleu ou en rouge de telle sorte qu’aucun des C(5,3) = 10 triangles ne soit monocolore. Voir figure n°3 ci-après

Il en résulte que la démonstration précédente ne s’applique pas et on peut aisément construire une configuration de 10 triangles dans laquelle il n’y aucun segment qui est en même temps le plus petit côté dans un triangle et le plus grand dans un triangle adjacent.

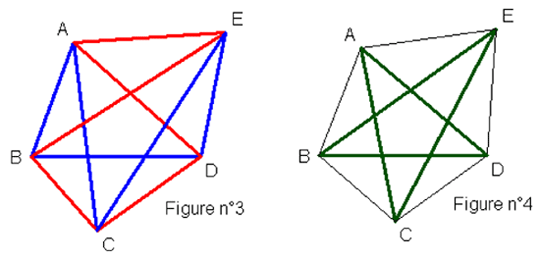
D’après la figure n°4, les plus petits côtés des triangles sont les côtés du pentagone ABCDE tandis que les plus grands côtés sont les diagonales de ce même pentagone