Solution au problème d'octobre 2007
Le problème:
Un cercle de centre O et de 1 cm de rayon roule à
l'intérieur d'un
triangle dont les côtés mesurent 6, 8 et 10 cm
respectivement,
en longeant les côtés. Quelle distance O parcourt-il en un
circuit
complet?
Nous avons pris ce problème d'une liste de
problèmes
du séminaire de concours mathématiques de Waterloo de
2002. Nous avons reçu des solutions correctes de
Felix Arnaiz Lanzo -- 2 solutions (Espagne) |
Matthew Lim (États-Unis) |
Gérard Billion (France) |
Jacques Mertzeisen (France) |
Ritwik Chaudhuri (Inde) |
Kacem Nouini (France) |
Sébastien Dumortier (France) |
Mark Pilloff (États-Unis) |
Baptiste Gorin -- 2 solutions (France) |
John T. Robinson (États-Unis) |
Xavier Hecquet (France) |
K. Sengupta (Inde) |
Normand LaLiberté (Ontario) |
A. Teitelman (Israël) |
Farid Lian Martínez (Espagne(?)) |
Philippe Fondanaiche (France) |
Solution.
Nos correspondants ont d'abord observé que le centre O
décrit un triangle dont les côtés sont
parallèles au triangle original. Le problème se
réduit
alors à trouver le rapport d'homothétie entre ABC et
A'B'C'. Nos correspondants ont
utilisé plusieurs méthodes intéressantes pour
démontrer que ce rapport est ½, donc la distance
parcourue par O est la moitié du périmètre du
grand
triangle, soit ½(6 + 8 + 10) = 12. Voici quelques unes de
leurs solutions.
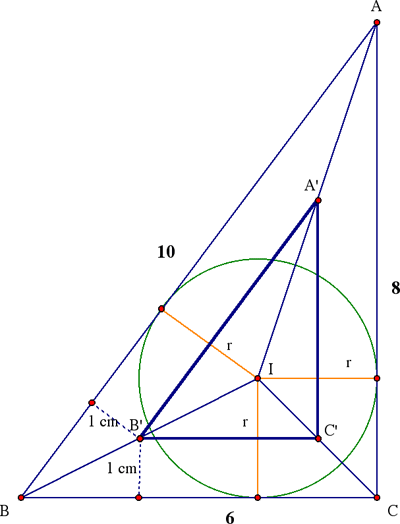
Méthode 1.
Nous reproduisons ici la version de Mertzeisen de la solution la plus
populaire.
Les droites définies par les
paires de sommets homologues des deux triangles sont
(évidemment?) les bissectrices des angles du triangle ABC. Soit
I le centre du cercle inscrit. Les côtés des deux
triangles étant respectivement parallèles, I est centre
d'une homothétie transformant le grand en le petit.
Soit R le rayon
du cercle inscrit et P le périmètre du triangle. L'aire S
du triangle ABC égale la somme des aires des triangles AIB, BIC
et CIA: S = PR/2 d'où R = 2S/P. Ici R = 48/24 = 2. Le rapport d'homothétie (R-r)/R
est ici égal à 1/2.
Le périmètre du petit triangle est 12 cm.'
Méthode 2
Un cercle de centre O et de 1 cm de rayon
roule à l'intérieur d
(Billion).
Calculons
le
rayon r du cercle inscrit dans un triangle ABC rectangle en C.
En
considérant
les médiatrices et les normales aux cotés passant par
le centre du cercle inscrit on constate que AB = ( AC – r ) + ( BC
– r ) donc r = ( AC + BC – AB ) / 2
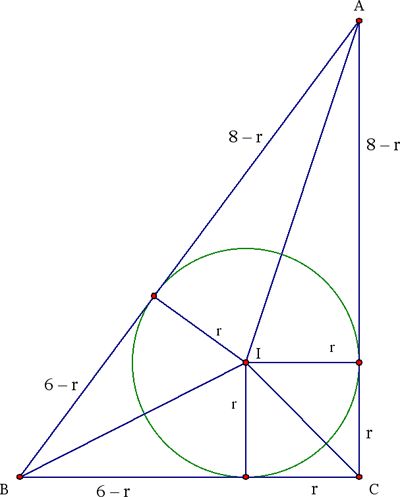
Un cercle de centre O et de 1 cm de rayon
roule à l'intérieur d
Le centre du cercle de
rayon 1 cm
décrit un triangle dont les côtés sont
parallèles
aux côtés du triangle ABC et dont les sommets se trouvent
sur
les médiatrices du triangle ABC.
Un cercle de centre O et de 1 cm de rayon
roule à l'intérieur d
Ces deux triangles sont semblables et
en appliquant le théorème de Thalès on peux
calculer le
rapport d’homothétie entre ces deux triangle et donc entre
les deux périmètres : (r-1) / r.
Ici, r =
(8+6-10)/2 = 2 cm et distance parcourue par O est (10+6+8)*[(2-1)/2] = 12 cm
Méthode 3. Cinq
des solutions utilisaient la trigonométrie, comme par exemple
celle de Normand Laliberté.
La
distance parcourue en un circuit complet est de 12 cm.
Observons
que:
Comme
62 + 82 = 102, le triangle ABC est
rectangle en C; AB = 10, BC = 6, AC = 8.
Le
circuit décrit par le cercle O est constamment parallèle
à, et à distance 1, de chacun des côtés de
ABC tour à tour; il forme donc un triangle DEF semblable
à
ABC, rectangle en F.
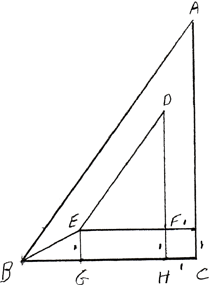
Comme E est à
distance 1 des côtés AB et BC, la ligne
BE est bissectrice de l'angle ABC que nous dénotons B.
Nous
avons:
cos
B = 6 / 10 = 3 / 5
Soit
la formule de linéarisation
tan2 a = (1 – cos 2a) / (1 + cos 2a)
Nous
obtenons pour l'angle a = B/2:
tan2 B/2 = (1 – 3/5) / (1 + 3/5) = 1/4
D'où:
tan
B/2 = 1/2
Soit
G la projection orthogonale de BB' sur BC; nous avons B'G = 1
Soit
H la projection orthogonale de BF sur BC; nous avons FH = CH = 1
D'où:
EG
/ BG = tan B/2 = 1/2
Comme
EG = 1, nous obtenons BG = 2.
Mais:
6
= BC = BG + GH + HC = 2 + GH + 1
D'où:
GH
= EF = 3
Comme
ABC et DEF sont semblables, il s'en suit que DF = 4, DE = 5. Donc le
périmètre de DEF –le parcours du cercle O- est 12.
QED
l'hypoténuse de 5/4 cm.
Donc BJ fait 3/4 cm, JH fait 5/4 cm, et KC fait 1cm; HK mesure donc 6 –
2 – 1 = 3 cm.

