Solution au problème de janvier 2008

Le problème:
	Quels sont les entiers positifs n tels que 3n + 4n + ... + (n+2)n = (n+3)n ?

La solution:

Nous avons reçu des solutions correctes de

Saïd Amghibech (Québec)	Matthew Lim (États-Unis)
Timothy Calford (Ontario)	Jacques Mertzeisen (France)
Dan Dima (Roumanie)	Viktor Pačnik (Slovénie)
Philippe Fondanaiche (France)	John T. Robinson (États-Unis)
Xavier Hecquet (France)	Heri Setiyawan (Indonésie)

    L'identité est valide seulement lorsque n vaut 2 ou 3. En effet,
on a 3² + 4² = 5² et 3³ + 4³ + 5³ = 6³. Mais à partir de n = 4 on observe un écart entre la somme de gauche (G_n) et le terme de droite (D_n):

On remarque que l'écart se creuse entre G_n et D_n, ce qui peut donner l'idée d'employer l'induction, comme l'a fait Hecquet. Nous reproduisons ici sa solution.

"Supposons qu’il existe n tel que :

Ajoutons (n+3)ⁿ des deux côtés :

Multiplions de part et d’autre par (n+3)

Étudions maintenant le rapport suivant :

 

Or, en se limitant aux premiers membres du développement du terme en puissance (ordre 2 à gauche et ordre 1 à droite):

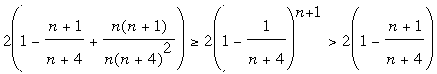
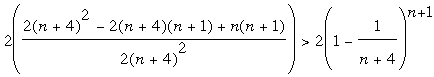
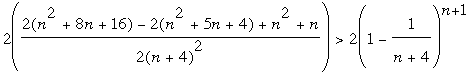
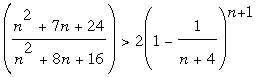
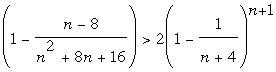
Donc, pour n ≥ 8, on est certain que notre expression est inférieure à 1. Donc que
2(n+3)ⁿ⁺¹ < (n+4)ⁿ⁺¹.

Donc , par récurrence, on en déduit que si la somme étudiée à gauche est inférieure au terme de droite, sa grande soeur (en n+1) le sera aussi (par rapport au terme en n+1).''

Commentaire:

Notons que le développement de 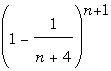par la formule du binôme de Newton donne

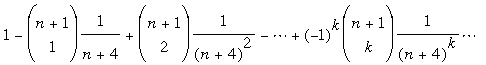
Comme 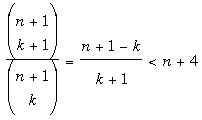, les termes décroissent en valeur absolue, ce qui justifie l'inégalité employée par Hecquet.