|
Solution au problème de février 2008
| Le problème: |
 |

Un plan vertical contient un cercle et un point P situé à l'extérieur du cercle et au dessus de la ligne horizontale sur laquelle celui-ci repose. Votre mission est de tendre un fil en ligne droite de P à un point Q sur le cercle, de telle sorte qu'un écrou glissant sur le fil atteigne le cercle le plus rapidement possible. La seule force agissant sur l'écrou est la gravité. Le chemin le plus court suit un fil qui relie P au centre du cercle, et le chemin le plus à pic est tangent au cercle. Entre les deux se trouve un chemin qui combine de façon optimale la distance et la vitesse, et votre tâche est de le trouver.
Quelques souvenirs du collège vous seront utile:
- Selon Newton, la relation au temps t entre la distance s et la vitesse v d'un écrou soumis à une accélération constante est s = 1/2 vt.
- Si m est la masse de l'écrou, g la constante de gravité et h la composante verticale de la distance de P à Q, alors l'énergie potentielle mgh de l'écrou au point P vaut 1/2 mv2, où v est sa vitesse au point Q.
- Bien sûr, on ignore la friction de l'air et du fil.
|
La solution:
Nous avons reçu des solutions correctes de Gérard Billion (France), Philippe Fondanaiche (France), Farid Lian Martinez (Colombie), Richard McIntosh (Regina), Jacques Mertzeisen (France), Matthew Lim (États-Unis), Giovanni Parzanese (Italie), John T. Robinson (États-Unis). Nous reproduisons ici les solutions de Philippe Fondanaiche et de Gérard Billion.
Solution de Philippe Fondanaiche:
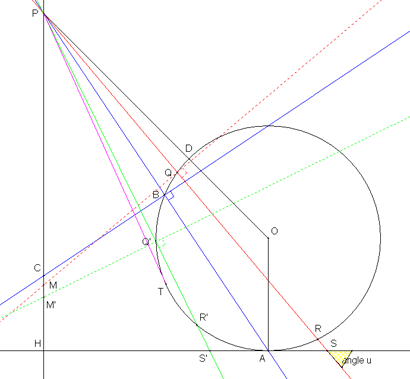
Notations : Le cercle de centre O est tangent en A à l’axe horizontal des abscisses. Soit H la projection de P sur cet axe. PO rencontre le cercle en un point D est qui est le plus proche de P. La droite PQ en rouge coupe le cercle en un deuxième point R et l’axe des abscisses au point S. On a tracé en vert la droite PQ’R’S’ quand le point S passe à gauche de A pour devenir S’. La droite PA en bleu rencontre le cercle en un deuxième point B. La perpendiculaire en B à PB rencontre la droite PH au point C. La tangente au cercle issue de A qui est la plus pentue rencontre le cercle au point T.
Si on désigne par u l’angle que fait la droite PQ avec l’axe horizontal des abscisses, l’écrou est soumis le long de PQ à une accélération égale à g*sin(u) et l’on a la relation 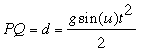 en supposant que la vitesse initiale de l’écrou est nulle. Dès lors le temps t mis par l’écrou pour atteindre le cercle est proportionnel à la racine carrée de en supposant que la vitesse initiale de l’écrou est nulle. Dès lors le temps t mis par l’écrou pour atteindre le cercle est proportionnel à la racine carrée de 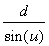 Or cette dernière quantité est égale au segment PM avec M à l’intersection de la verticale PH avec la perpendiculaire en Q à la droite PQ. Le problème revient donc à minimiser la longueur de PM quand Q va de D à T. Il est préférable de s’en tenir à des raisonnements purement géométriques simples. Or cette dernière quantité est égale au segment PM avec M à l’intersection de la verticale PH avec la perpendiculaire en Q à la droite PQ. Le problème revient donc à minimiser la longueur de PM quand Q va de D à T. Il est préférable de s’en tenir à des raisonnements purement géométriques simples.
Le point recherché sur le cercle est le point B et le minimum de PM est obtenu quand M vient en C. En effet quand S est à droite du point A, on a PQ*PS = PM*PH car les points Q,S,H et M sont cocycliques, le quadrilatère QSHM ayant deux angles droits en H et Q. Or PQ*PS > PQ*PR = PT2 =PA*PB = PC*PH. Il en résulte que PM*PH >PC*PH. D’où PM>PC. Quand S’ est à gauche du point A, on obtient de la même manière PQ’*PS’ > PQ’*PR’ = PT2 = PA*PB = PC*PH. D’où PM’>PC.
Solution de Gérard Billion:
Dans le même temps que l’écrou glisse de P vers Q, un autre écrou lâché en P tomberait verticalement de P jusqu’à un à point R. Les distances PQ et PR sont liées par la relation PQ = PR.Cos(Theta), avec Theta l’angle entre la verticale et l’axe PQ. Le point Q atteint le plus rapidement correspond donc au point R le plus haut.
Le Triangle PQR est rectangle en Q. Donc PR est un diamètre du cercle circonscrit à PQR. Le Point Q optimum est donc obtenu lorsque le cercle circonscrit à PQR est tangent en Q au cercle initial. Soit R’ le point du cercle initial situé à la verticale et en dessous du centre de ce cercle, d’après le théorème ci-dessous le point Q du chemin qui combine de façon optimale la distance et la vitesse est donc l’intersection de PR’ et du cercle initial.
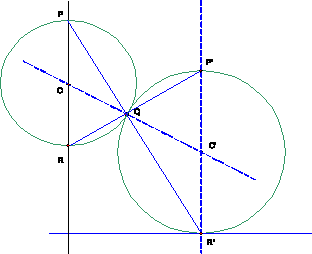
Théorème : Soit deux cercles quelconques non inclus l’un dans l’autre, tangents en Q, PR un diamètre du premier cercle et P’R’ un diamètre du second cercle parallèle et de même sens que PR, alors P,Q & R’ sont alignés ainsi que P’,Q & R.
Démonstration : Soit O le centre du premier cercle, et O’ le centre du deuxième.
O,Q et O’ sont alignés, donc angle(POQ)=angle(QO’R’) donc le triangle PQR est semblable au triangle P’QR’, angle(OPQ)=angle(O’R’Q) et angle(ORQ)=angle(O’P’Q). Donc P,Q & R’ sont alignés ainsi que P’,Q et R.
|

