Solution au problème de décembre 2007

Le problème:

Pour le temps des fêtes, nous vous proposons un tour de magie pour épater tous vos parents et amis qui recevront une pitonneuse en cadeau. (Note pour nos correspondants internationaux: "pitonneuse'' est un terme canadien qui désigne une calculatrice de poche.) Dites leur de choisir un nombre, n'importe quel nombre entre 1 et 1000. Appelons le N. Demandez leur ensuite de pitonner 1 plus 1/N plus le double de la racine carrée de 1/N, d'extraire la racine carrée du résultat et de la mettre en mémoire en appuyant sur le bouton M+. Puis demandez leur de pitonner 1 plus 1/N moins le double de la racine carrée de 1/N, d'extraire la racine carrée du résultat et de l'ajouter en mémoire en appuyant sur le bouton M+. Enfin, demandez leur d'extraire le résultat en mémoire en appuyant sur le bouton MR. (Ce résultat est bien sûr la somme des racines calculées aux étapes 2 et 3). En même temps, sortez une enveloppe scellée de votre poche et dites leur de l'ouvrir. Lorsqu'ils verront le nombre à l'intérieur, dites leur "C'est le nombre que vous avez obtenu, non?'' Bien sûr, vous devez préparer l'enveloppe scellée à l'avance. Notre problème du mois est: Quel nombre magique devrez vous mettre à l'intérieur, et pourquoi est-ce que ça marche?

La solution:

Grâce à la magie de l'internet, nous avons reçu des solutions de correspondants partout dans le monde:

Theerasak  Asawanonwiwat (Thaïlande)	Suma Iyer (Inde)
Ricardo Barroso Campos (Espagne)	Kacem Nouini (France)
Bojan Basic (Serbie)	Wolfgang Kais (Allemagne)
Gérard Billion (France)	Imad Mohamed Khan (Inde)
Alicia Bretón (internet)	Normand LaLiberté (Ontario)
Lou Cairoli (États-Unis)	Marc Lichtenberg (France)
K.A. Chandrashekara (Inde)	Jean-Luc Luyet (Suisse)
Dave Denison (États-Unis)	Jacques Mertzeisen (France)
Sébastien Dumortier (France)	Nikhil V. Nair (Inde)
Philippe Fondanaiche (France)	Viktor Pačnik  (Slovénie)
Alenka Gabrovec (Slovénie)	Wilfrid Pillard (France)
Xavier Hecquet (France)	John T. Robinson (États-Unis)
Armando Huayanca (Pérou)	Brian Six (États-Unis)
Rizwan A Hussain (Îles Fidji)	Steve Sparling (Colombie Britannique)
Yitz Itzik (internet)	A. Teitelman (Israël)

De plus, le bon vieux facteur nous a livré la jolie carte de Luyet:

Comme plusieurs de nos correspondants, Luyet s'est servi de la mise au carré, qui permet de simplifier tous les termes variables comme par magie. Notons que cette astuce utilise l'identité

√a · √b = √(a · b),

qui est ici valide puisque les termes sont positifs. Dans le cas de termes négatifs, cette identité a la fâcheuse manie de rendre possible l'impossible, comme dans

√-1 · √-1 = √(-1 · -1) = √1 = 1.

Même en utilisant les nombres complexes, on peut transformer magiquement le négatif en positif avec cette identité:

-1 = i · i = √-1 · √-1 = √(-1 · -1) = √1 = 1.

Quoiqu'il en soit, certains de nos correspondants ont préféré se servir de la factorisation. Nous reproduisons ici la solution de Mertzeisen.

"Soit N un nombre compris entre 1 et 1000. Alors

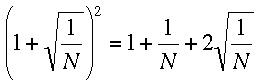
et

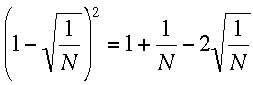
On remarquera que si N ≥ 1, alors 1 + 1/N et 1 - 1/N existent et sont tous deux positifs donc

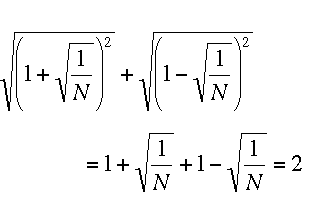
Notre pitonneur cumule les valeurs approchées de ces deux racines carrées dans la mémoire de son outil. Il n’est donc pas étonnant qu’il obtienne 2 lorsqu’il en rappelle le contenu.

Avec la condition N ≤ 1000 le magicien s’est simplement assuré que la pitonneuse est capable de calculer ce résultat avec une précision suffisante.''

Au sujet de la précision, Laliberté commente "Je ne saurais dire avec quelle précision la pitonneuse va afficher le résultat lorsque N est entier et 1 ≤ N ≤ 1000; c'est-à-dire ni si, ni pourquoi il sera arrondi à 2. Le fonctionnement de ces bidules est un mystère pour moi.''

En fait, la précision du bidule est variable. Les pitonneuses bon marché ont des erreurs d'arrondi alors que les pitonneuse respectables donnent la bonne valeur de 2, même avec des valeurs fractionnaires de N comme N = 1.1 ou N = 1.01. Qu'en est-il des logiciels scientifiques? Maple 11 donne 2 lorsque N est un entier entre 1 et 1000, mais donne 1.999999993 lorsque N = 1.1, et 2.000000052 lorsque N = 1.01. Un vrai mystère!

Enfin, notons que certains correspondants ont postulé que le Problème du Mois n'allait tout de même pas humilier ses correspondants en leur proposant un tour de magie qui rate à tout coup. Ils se sont donc contentés de trouver la valeur de 2 en faisant le calcul avec N = 1. C'est très gentil, une grande marque de confiance envers nous. Par contre, ce n'est pas une démonstation mathématique complète. Mais en cette saison des fêtes, nous préférons ne pas leur en tenir rigueur.

Source. Notre problème du mois est une adaptation du Problemath 2 (17 septembre 2007) de l'Unité de Recherche sur l’Enseignement des Mathématiques de l'Université Libre de Bruxelles:

Existe-t-il deux nombres réels a et b (a < b) tels que la valeur de l'expression

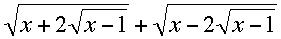
soit constante pour tout x dans l’intervalle fermé [a,b]?

Maple 11 réussit tout de même à tracer le graphe de l'expression:

On note que la courbe s'aplatit magiquement à gauche de x = 2. Notre tour de magie est obtenu en posant x = 1 + 1/N.