|
Solution au problème d'avril 2008
| Le problème: |
 |
Soit a, b et c, des entiers positifs dont le
seul diviseur commun est 1 (aucun entier supérieur à 1 ne
divise les trois).
Démontrez que si
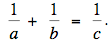
alors (a + b),
(a – c) et (b – c) sont des carrés parfaits.
|
La solution:
Ce problème est tiré de Problem of the Week 1094 (27 mars 2008), édité par Andrew Beveridge à
Macalester College, St. Paul, Minnesota; sa source était School
Science and Mathematics 63 (octobre 1963), p.
60. Nous avons reçu des solutions correctes de
Bojan Basic (Serbie) |
Wolfgang Kais (Allemagne) |
Gérard Billion (France) |
Normand LaLiberté (Ontario) |
Lou Cairoli (États-Unis) |
Matthew Lim (États-Unis) |
John Campbell (Alberta) |
Richard McIntosh (Regina) |
Olivier Cyr (France) |
Jacques Mertzeisen (France) |
Dan Dima (Roumanie) |
Giovanni Parzanese (Italie) |
Philippe Fondanaiche (France) |
Ananda Raidu (Inde) |
Mudit Goel (Inde) |
John T. Robinson (États-Unis) |
Xavier Hecquet (France) |
K. Sengupta (Inde) |
|
A. Teitelman (Israël) |
Nous avons aussi reçu trois solutions partielles.
Nous reproduisons ici la solution de Xavier Hecquet.
"En multipliant par abc tout partout, on obtient donc : bc + ac = ab
Calculons, pour le fun :
(a + b)(a - c) =a² + ab - ac - bc = a²
(a + b)(b - c)=ab + b² - ac - bc = b²
(a - c)(b - c)=ab - bc - ac + c² = c²
Pour tout p diviseur de c, on aura : p ne peut diviser a et b. Donc, p ne pourra diviser simultanément (a - c) et (b - c).
Or (a - c)(b - c)=p²K² (en posant c = pK)
Donc, comme p n’est diviseur que d’un des membres de gauche, on en déduit que p² divise (a - c) ou (b - c). En itérant cela sur l’ensemble des diviseurs de c, on en déduit que (a - c) est le produit des carrés de certains diviseurs de c, et parallèlement, (b - c) est également le produit des carrés des autres diviseurs de c.
Je serai tenté de dire que : (a + b)(a - c) = a², or, (a - c) est un carré, donc (a + b) est un carré. C’est peut-être un peu rapide. Sinon, on refait le même raisonnement que pour (a - c)(b - c), en prenant en compte les diviseurs de a (resp. de b).
Remarque : Juste histoire d’étaler mes grandes connaissances (de Google J), il est évident que 1/a+1/b=1/c, ça m’a tout de suite fait penser à la moyenne harmonique dans un trapèze :
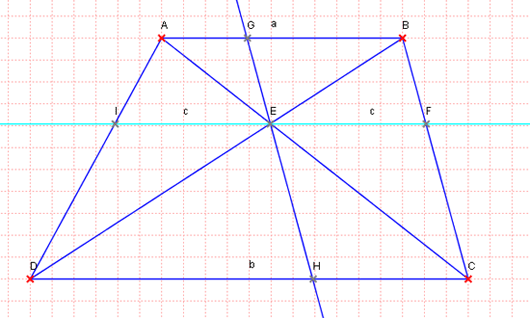
En l’occurrence, en posant AB=a, DC=b et EF=c, on a bien 1/a+1/b=1/c (sisi, avec des vrais morceaux de Thalès dedans, on y arrive).
En portant la parallèle à (BC) en E, on voit tout de suite, sans faire de calcul, et hop, que :
AG/c=c/DH, et donc AG.DH=c²=(a-c)(b-c).''
Commentaires: D'autres solutions sont disponibles sur notre page anglaise, notamment celle de Richard McIntosh qui relie le problème au dernier théorème de Fermat.
|

