|
Solution au problème
d'octobre 2006
Votre mission est de transformer
x2 + 10 x + 20 en x2 + 20 x + 10
en au plus 50 étapes. À chaque étape vous pouvez
ajouter ou soustraire 1, du coefficient de x ou bien du terme
constant (pas les deux en même temps).
De plus,
aucun des polynômes intermédiaires de doit admettre
une factorisation
de la forme (x+m)(x+n), où m et n sont entiers.
Par exemple, on ne peut changer le 10 en 9 à la première
étape, parce que
x2 + 9x + 20 = (x+5)(x+4).
SOURCE: Notre problème d'octobre est tiré de Edward
J. Barbeau, Polynomials (Springer, 1989), page 41 #6.
Nous
avons reçu des solutions correctes de
Mario Antunez (Honduras) |
|
Wolfgang Kais (Allemagne) |
| Quinn Barber (Alberta) |
|
Matthew Lim (États-Unis) |
| Pierre Bornsztein (France) |
|
Patrick LoPresti (États-Unis) |
| Bernard Carpentier (France) |
|
Juan Mir Pieras (Espagne) |
| K.A. Chandrashekara (Inde) |
|
Wilfrid Pillard (France) |
| Sébastien Dumortier (France) |
|
Torin Stepan (Alberta) |
| Philippe Fondanaiche (France) |
|
A. Teitelmam (Israël) |
| Xavier Hecquet (France) |
|
|
Solution.
Nos correspondants
se sont écriés en choeur "Mission Impossible!" et ils ont
bien raison: en 50 étapes ou plus on ne peut jamais passer du premier
polynôme au second. Que voulez-vous? Le problème du mois vieillit,
et il devient ratoureux avec l'âge. Fondanaiche note que la tâche
à réaliser s'apparente selon l'humeur à la confection
de la tapisserie de Pénélope ou à la remontée
du rocher de Sisyphe.
Il y a deux façons de démontrer que la tâche
est impossible.
La solution algébrique. Nous reproduisons ici la
solution de Bernard Carpentier:
Les polynômes
sont de la forme x² + bx + c; x = -1 est racine lorsque 1 - b + c
= 0 c'est à dire lorsque b = c + 1. Or b passe de 10 à
20 et c passe de 20 à 10 par pas de 1 non simultanés. Donc,
lors d'une étape, b dépassera c de une unité. Alors
b = c + 1, donc fatalement x = -1 sera racine entière à cette
étape (la factorisation étant (x+1)(x+c)).
La solution géométrique. (Basée sur la solution
de Mir, avec des idées tirées d'autres solutions similaires.)
Faisons correspondre
au polynôme x2 + px + q la case de
coordonnées (p, q) sur un échiquier infini. Notre
polynôme se déplace comme une tour pas pressée: un
p'tit coup à gauche, un p'tit coup à droite, un p'tit coup
en haut, un p'tit coup en bas, mais jamais en diagonale. On colorie en
rouge les cases correspondant aux polynômes qui admettent une factorisation
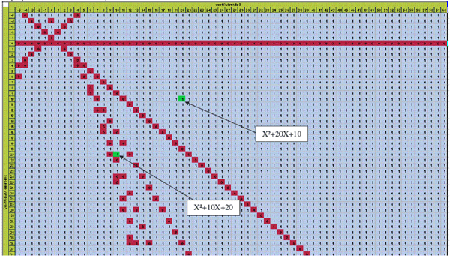
(x + m)(x + n), où m et n sont entiers, comme dans l'illustration de Dumortier ci-bas. Notre tâche
est de déplacer la tour de la case (10,20) à la case (20,10),
sans passer par une case rouge, mais c'est impossible puisqu'entre ces
deux cases il y a toute une diagonale (q+1, q) de cases rouges.
Commentaire. Hecquet propose la conjecture suivante:
"Je n'ai pas trop le temps de mettre réellement au point la chose,
mais on doit obtenir le même genre de résultats en considérant
des polynômes en x^3+ax²+bx+c non factorisables en (x-p)(x²+gx+h).
Potentiellement avec toute dimension, aurais-je même l'impertinence
de suggérer..."
Hmmmmm, peut-être cette mission là est-elle possible?
|

