Solution au problème de mars 2007

Le problème:
	Démontrez qu'il existe une infinité de nombres N tels que             (i) N est divisible par la somme de ses chiffres, et             (ii) aucun des chiffres de N est zéro.

Réponses correctes:

Il s'agit du problème 3 de l'Olympiade Mathématique Canadienne de 1984. Nous avons reçu des solutions correctes de Mohamed Benchaib (Maroc) Matthew Lim (États-Unis) Gérard Billion (France) Jean-Luc Luyet (Suisse) Lou Cairoli (États-Unis) Mark Pilloff (États-Unis) Dan Dima (Roumanie) Joseph Najnudel (France) Philippe Fondanaiche (France) Ananda Raidu (Inde) Zac Friggstad (Edmonton) John T. Robinson (États-Unis) Xavier Hecquet (France) K. Sengupta (Inde) Wolfgang Kais (Allemagne) Heri Setiyawan (Indonésie) Normand LaLiberté (Ontario)

La solution:

Les solutions soumises étaient basées sur les règles de divisibilité par les puissances de 2, 3 et 5. L'approche la plus commune, qui est aussi celle du solutionnaire officiel de l'Olympiade Mathématique Canadienne, est de coller côte à côte trois copies d'un nombre qui est un multiple de la somme de ses chiffres. Nous reproduisons ici la solution de Gérard Billion.

"Si on génère un nombre en répètant trois fois la succession des chiffres d'un nombre vérifiant ces deux conditions on obtient un nouveau nombre vérifiant ces conditions, donc il existe une infinité de tels nombres.

Soit N un nombre de n chiffres vérifiant les deux conditions (soit S la somme de ses chiffres), soit NN le nombre généré à partir de N (SS la somme de ses chiffres), nous avons :

NN = N ( 1 + 10ⁿ+ 10²ⁿ ) et bien sûr SS = 3S

3 divise ( 1 + 10ⁿ+ 10²ⁿ ) et S divise N  donc 3S divise N ( 1 + 10ⁿ  + 10²ⁿ ) donc SS divise NN.

(par exemple 12 divisible par 3 donne 121212=10101*12 divisible par 9)''

Généralisation de Matthew Lim.
L'argument ci-haut est valide dans toute base b supérieure à 2, apres une légère modification: Plutôt que d'utiliser 3 copies du nombre initial, on en utilise d, où d est un facteur de b-1. Lim démontre que si S est la somme des chiffres du nombre initial représenté en base b, alors la juxtaposition de d^k copies du nombre initial divise s·d^k, qui est la somme de ses chiffres. Il démontre  aussi que la base 2 est une exception: Un nombre en base 2 qui ne contient pas le chiffre 0 est une chaîne de 1s, qui vaut 2^k – 1. La somme des chiffres binaires de 2^k – 1 est k, mais avec un peu de théorie des nombres, on peut démontrer que pour k > 1, k ne divise pas 2^k – 1.

L'approche de Jean-Luc Luyet.
La solution de Luyet est basée sur une astuce différente. Nous la reproduisons ici.

"L'algorithme est fondé sur le fait que 10ⁿ = 2ⁿ 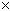5ⁿ, ce qui a pour  conséquence immédiate que

Un nombre entier est divisible par 2ⁿ si et seulement si ses n derniers chiffres sont divisibles par 2ⁿ.

Mais la somme des chiffres d'un nombre composé de n chiffres ne peut  dépasser 9xn et comme on a pour tout n > 5 que 9 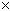n < 2ⁿ, on sait que la somme des chiffres d'un nombre à n chiffres sera toujours inférieure à  2ⁿ (si n vaut au moins 6). Il suffit donc de trouver un multiple de  2ⁿ qui a n chiffres, et de lui rajouter des 1 devant, jusqu'à ce que  la somme des chiffres atteigne 2ⁿ pour obtenir un nombre qui remplit  la condition d'être divisible par la somme de ses chiffres.

Ce qui suit est juste la preuve technique que c'est toujours possible  de construire un tel nombre qui ne contient pas de zéro.

Une puissance de 2 ne se termine jamais par zéro (sinon elle serait  divisible par 10 et donc par 5, mais c'est impossible puisque c'est  une puissance de 2). En revanche, peut-être que parmi les autres  chiffres se trouvent des zéros. Supposons qu'il y ait un zéro à la  k-ième place en partant de la fin du nombre, on considère alors 2ⁿ +  (10^k-1 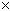2ⁿ) ce qui a pour effet de remplacer ce zéro par le  dernier chiffre de la puissance de 2. On continue ainsi jusqu'à  obtenir un nombre dont les n derniers chiffres sont tous différents de  zéro.

Ce nombre est un multiple de 2ⁿ, donc si on garde seulement les n  derniers chiffres, le nombre obtenu sera également un multiple de 2ⁿ  qui aura la propriété de n'avoir aucun zéro. On fait la somme S de ses  chiffres et l'on rajoute (2ⁿ-S) chiffres 1 devant ce nombre. Voilà.

Exemple avec n=9 et n=10.

n=9 : 2⁹ = 512, le quatrième chiffre depuis la fin est un zéro (en  effet, 512 = 0512). On rajoute donc 10³ 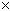512, et on obtient 512512. Le  septième chiffre depuis la fin est un zéro, on continue donc et on  obtient 512512512. C'est un nombre à 9 chiffres, dont les 9 derniers  chiffres sont différents de zéro. La somme de ses chiffres fait 24, il  faut donc rajouter 512-24 = 488 chiffres 1 devant. On obtient  finalement 111111111...1111512512512 dont la somme des chiffres est  512 et qui est bien divisible par 512.

n=10 : 2¹⁰= 1024, le troisième chiffre est zéro, il faut donc ajouter  102400, on obtient 103424. Le cinquième chiffre est zéro, on fait donc  103424 + 10240000 = 10343424. L'étape suivante amène à 1034343424 puis  à 103434343424. Même si ce nombre contient toujours un zéro, ce n'est  pas grave parce qu'on ne va garder que ces 10 derniers chiffres  3434343424, et on sait que ce nombre est divisible par 1024. Il suffit  de rajouter 990 chiffres 1 pour obtenir un nombre satisfaisant la  condition.''