Solution au problème de décembre 2006

Pour le temps des fêtes, le problème du mois vous propose un tour de magie pour les réunions familliales, qui ne nécessite aucun entrainement, et qui devrait ne laisser personne indifférent. Il suffit d'avoir une table de cuisine et 45 pièces de monnaie.

Vous placez les 45 pièces sur la table et vous vous bandez les yeux, puis vous demandez à un volontaire de répartir les pièces en autant de piles qu'il veut. Il peut par exemple faire une pile de 24 pièces, une pile de 20 pièces et une pile de une pièce. Dites-lui de prendre une pièce de chaque pile pour faire une nouvelle pile. (Ce qui donne, dans notre exemple, une pile de 3 pièces en plus des piles de 23 et 19 pièces qui restent.) Dites lui maintenant de répéter le processus, c'est-à-dire de prendre une pièce de chaque pile (y compris la nouvelle) pour former une nouvelle pile. (Ce qui donne des piles de 22, 18, 3 et 2 pièces dans notre exemple.) Demandez-lui de répéter le processus plusieurs fois de suite, pendant que vous allez bavarder avec tante Ursule au salon.

Revenez dans la cuisine au bout d'une bonne vingtaine de minutes, les yeux toujours bandés (faites attention de ne pas vous cogner aux meubles), et annoncez à votre volontaire qu'il a maintenant neuf piles comprenant respectivement 1, 2, 3, 4, 5, 6, 7, 8 et 9 pièces.

Notre question du mois: Démontrez que ce tour fonctionne toujours.

(Si, en passant, vous trouvez une borne supérieure sur le nombre de répétitions du processus qui sont nécessaires pour obtenir la configuration finale, vous pouvez du même coup augmenter le prestige du tour en réduisant la charge de travail de ce pauvre volontaire.)

Nous ne connaissons pas l'origine de ce problème. Il nous a été communiqué par Igor Astapov du département de Physique du Collège Militaire Royal du Canada, qui l'a appris sur un site russe de clavardage mathématique.

Nous avons reçu des solutions correctes de

Merci beaucoup à Philippe Fondanaiche qui nous a fourni des informations et des références sur ce problème. Il s'agit du ``solitaire bulgare'', popularisé par Martin Gardner dans sa chronique ``Mathematical Games'' [Scientific American 249 (août 1983) pages 18-21].  Philippe Fondanaiche anime le site de récréations mathématiques Diophante (www.diophante.fr), dont le problème H101 portait sur le solitaire bulgare. Il nous a aussi indiqué le site www.augsburg.edu/math/faculty/doree/bulgarian_solitaire_bib.pdf qui contient plusieurs références inspirées par l'article de Gardner. On trouve aussi des indications dans l'article Wikipedia en.wikipedia.org/wiki/Bulgarian_solitaire.

Solution.  Il suffit de former la nouvelle pile en prenant une pièce du bas de chaque pile, de placer la nouvelle pile à gauche et  de décaler les anciennes piles d'une unité vers la droite. Formellement, si les pièces de la pile k occupent les positions (k,0), (k,1), ..., (k,h_k-1) du plan cartésien, le processus se déroule en trois étapes:

    1 - Les pièces qui étaient en position (x,0) vont à la position (0,x).
    2 - Les pièces qui étaient en position (x,y) où y est supérieur à 1 vont à la position (x+1,y-1).
    3 - N'oublions pas l'effet de la gravitation: une pièce en position (0,y) peut retomber en position (0,y-s) si avant l'étape 1, il y avait s piles vides à gauche de la pile y.

Appelons ``énergie potentielle'' d'une pièce en position (x,y) la valeur x + y. Les étapes 1 et 2 n'altèrent pas l'énergie potentielle d'une pièce, et l'étape 3 peut seulement la diminuer. Donc en répétant le processus indéfiniment la configuration des piles de pièces atteindra son énergie potentielle minimale.

    Observation: Lorsque la configuration des piles de pièces a atteint son énergie potentielle minimale, si la droite x + y = h contient au moins une pièce, alors la droite x + y = h-1 en contient le maximum possible, soit h.

    En effet, soit une pièce notée  X  sur la droite x+y = h, et un trou noté O sur la droite x+y = h-1. Alors X et O se déplacent cycliquement du haut à gauche au bas à droite, la période de X est h+1 et celle de O est h.
Puisque ces deux périodes sont relativement premières, X va nécessairement passer au dessus de O et tomber, diminuant ainsi son énergie potentielle.

    Par suite,  lorsque la configuration a atteint son énergie potentielle minimale, les droites x+y = 0 à x+y = 8 sont saturées, et les piles contiennent respectivement 1, 2, ..., 9 pièces.

Commentaires.  Notre solution nous paraît plus simple que celles qui sont publiées. Par contre, nous ne savons pas si notre approche est toujours valide dans le vide intersidéral où la gravitation n'agit pas.  Fondanaiche nous a fait parvenir une solution plus complète qui donne toutes les configurations cycliques pour tout nombre n de pièces. Pour sa part, LoPresti propose une approche différente: ses pièces sont numérotées de 1 à 45, et après avoir mis la nouvelle pile à gauche, il réordonne les pièces de chaque pile en ordre croissant. Ainsi, après quelques itérations, la pièce 1 se retrouve dans le coin du bas à gauche, puis les pièces 2 et 3 dans la diagonale suivante, et ainsi de suite.  Dumortier, quant à lui, a choisi la manière forte: Il s'est servi d'un ordinateur pour effectuer le tour sur les 89134 partitions possibles de 45 pièces en piles de pièces. Dans tout les cas, en au plus 72 itérations au plus, les pièces se répartissaient en 9 piles comprenant respectivement 1, 2, 3, 4, 5, 6, 7, 8 et 9 pièces. Avec 6 pièces plutôt que 45, on peut voir l'action du processus dans l'arbre suivant:

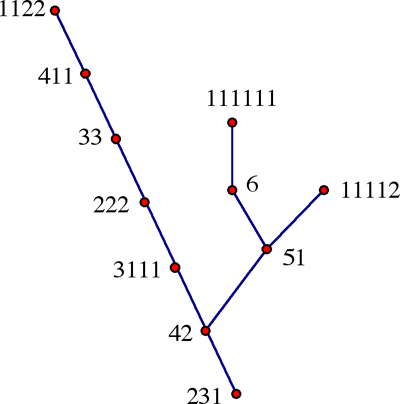
On constate que le processus répartit les pièces en piles de 1, 2 et 3 en au plus 6 itérations. Or, 6 = 2x3 tout comme 72 = 8x9.  Il était conjecturé que pour le nombre triangulaire n = k(k+1)/2, au plus k(k-1) itérations sont nécessaires pour obtenir la configuration avec k piles de tailles différentes. Cette conjecture a été démontrée par Kiyoshi Igusa dans "Solution of the Bulgarian Solitaire Conjecture" [Math. Magazine 58:5 (November 1985) 259-271]. Nous ne savons pas si il existe une démonstration élémentaire de cette conjecture.