Solution au problème de septembre 2004
Sur le cercle unité, on marque les douze sommets d'un dodécaèdre régulier, et on relie ces sommets au centre du cercle, ce qui donne douze rayons. A partir d'un des douze sommets, on mène une perpendiculaire au prochain rayon en sens horaire; puis du pied de cette perpendiculaire, on mène une perpendiculaire au prochain rayon, et ainsi de suite.
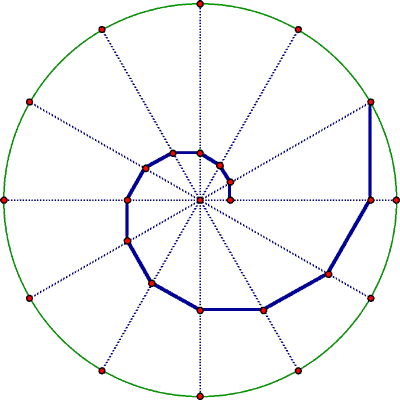
Quelle est la somme des longueurs de toutes ces perpendiculaires?
Solution au problème MP43
Nous avons reçu des solutions correctes de
| Alex Akulov (Regina) | Wolfgang Kais (Allemagne) |
| Said Amghibech (Québec) | Normand LaLiberté (Ontario) |
| Endre Balogh (Hongrie) | Patrick LoPresti (…tats-Unis) |
| Ricardo Barroso Campos (Espagne) | Marian Marinescu(France) |
| Pierre Bornsztein (France) | Juan Mir Pieras (Espagne) |
| Bernard Carpentier | Leigh Norris (…tats-Unis) |
| Bruno Demarest (France(?)) | Fernando Szechtman(Regina) |
| Xavier Hecquet (France) | AWD ‘Silversprite’ |
| Pablo de la Viuda (Espagne) |
Nous retrouvons avec plaisir plusieurs de nos vieux amis, ainsi que plusieurs nouveaux venus à qui nous souhaitons la bienvenue. Merci à tous pour vos solutions intéressantes. Tout le monde a calculé la somme d'une série pour déterminer que la longueur du chemin est
![]()
Après
la présentation de cette solution, nous examinerons
deux solutions géométriques de Xavier Hecquet et quelques généralisations
de Kais, Mir et Szechtmen.
La solution par la série
Notons O le centre et P0 le point initial sur le cercle unité. Soit P1, P2, ..., la suite des pieds des perpendiculaires successives. Les triangles OPnPn+1 sont tous des triangles rectangles ayant un angle de 30 degrés à O et de 60 degrés à Pn:
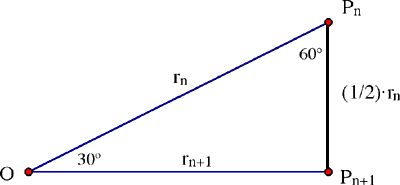
Par suite l'hypoténuse rn+1 = OPn+1 du triangle suivant s'obtient en multipliant par cos(30) = √3/2 l'hypoténuse rn de ce triangle, soit
![]()
La ligne polygonale dont nous calculons la longueur est formée des segments PnPn+1 ayant pour longueur rn sin(30) = rn /2. Par conséquent, la contribution du triangle suivant est
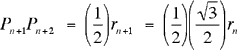
et la somme des longueurs des n+1 premiers segments est
P0P1 + P1P2 + P2P3 + ... + PnPn+1 = 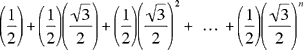
soit une serie géométrique de raison √3/2 dont la valeur est
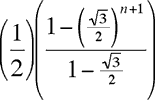
Puisque √3/2 < 1, (√3/2)n+1 tend vers 0 lorsque n tend vers l'infini, et la limite de la somme est
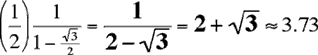
tel qu'annoncé.
Avec un peu de trigonométrie, on peut se passer de la formule de la somme en observant le diagramme approprié. Hecquet nous a envoyé deux de ces diagrammes.
Premier diagramme.
Ici, notre spirale est dépliée de façon à ce que les segments PnPn+1 soient colinéaires. Les triangles rectangles de ci-haut sont en bleu ci-bas, et le point O correspond à la suite de points O0, O1, O2, ...
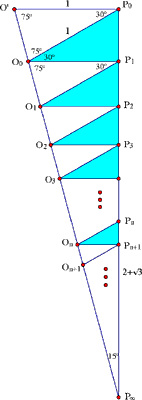
Or, puisque l'hypothénuse d'un triangle bleu a
la même
longueur que le côté du triangle bleu précédent,
les triangles OnPnOn+1 sont tous
isocèles, avec un angle de 30 degrés à Pn
et des angles de 75 degrés à On et On+1.
Par conséquent,
les points O0, O1, O2, ... sont
colinéaires. La droite passant par ces points coupe la
droite passant par P0, P1, ... en un point
qu'on note P![]() ,
et la longueur recherchée est celle du segment P0P
,
et la longueur recherchée est celle du segment P0P![]() .
Notons que ce segment est l'hypothénuse du triangle rectangle
P0P
.
Notons que ce segment est l'hypothénuse du triangle rectangle
P0P![]() O0,
qui a un angle de 15 degrés à P
O0,
qui a un angle de 15 degrés à P![]() ,
donc cos(15) = O0P0/P0P
,
donc cos(15) = O0P0/P0P![]() =
1/P0P
=
1/P0P![]() .
La longueur recherchée est donc
.
La longueur recherchée est donc
P0P![]() =
1/cot(150).
=
1/cot(150).
On peut vérifier que cette valeur est bien celle obtenue précédemment en utilisant la formule du demi-angle:
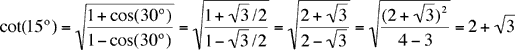
et
donc 1/cos(15) = 1/(2-√3) = 2 + √3.
Deuxième diagramme.
Nous alignons encore une fois les triangles, mais cette fois-ci tête-bêche, tel qu'illustré ci-bas.
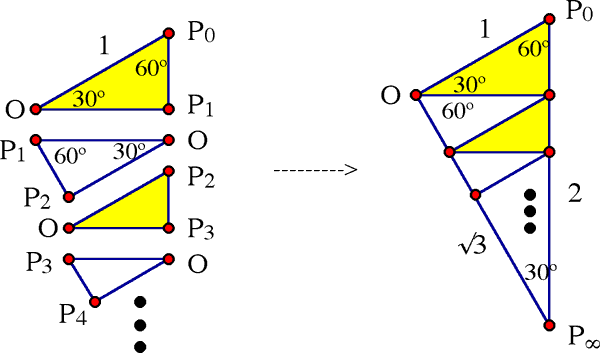
On obtient un triangle rectangle 30-60-90, et les segments constituant notre ligne brisée en recouvrent l'hypothénuse et le plus long côté. Puisque le côté opposé à l'angle de 30 degrés a une longueur de 1, l'hypothénuse et le plus long côté ont des longueurs respectives de 2 et √3, pour une longueur totale de 2 + √3.
Généralisations.
Il est facile d'adapter nos arguments au cas où le cercle
est divisé en n parties plutôt que douze. En général,
si l'angle PnOPn+1 est φ, la longueur du chemin sera 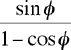 .
.
On peut aussi remplacer la perpendiculaire par un segment faisant un angle α avec la ligne suivante (où φ < α < 90). Le problème général peut donc être formulé comme suit:
Les points Q0, Q1, Q2, ... sont disposés régulièrement autour du cercle unité, et joints au centre O. On définit une ligne polygonale P0P1P2... récursivement en posant
P0 = Q0 et en plaçant Qn tel que l'angle Pn-1PnQn vaut α. Déterminez la longueur de la ligne polygonale P0P1P2...
Chacun des diagrammes de Hecquet s'adapte à une solution simple de ce probleme général. Les angles y sont modifiés comme suit
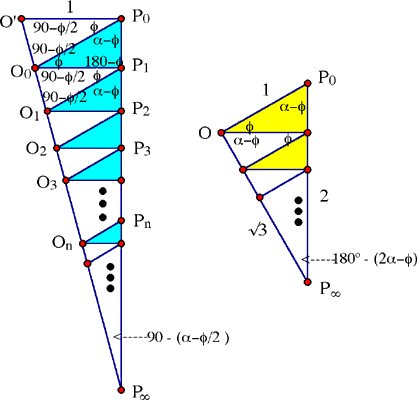
et on calcule la longueur des côtés désirés à l'aide de la loi du sinus, qui dit que dans un triangle quelquonque, le rapport du côté au sinus de l'angle opposé est le même pour les trois côtés. Avec le premier diagramme on obtient
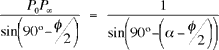
et avec le second
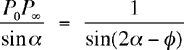 et
et 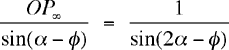
donc la longueur du chemin est P0 P![]() +
OP
+
OP![]() =
=  .
.
En prime, on a l'identité trigonométrique qui découle de la validité des deux approches:
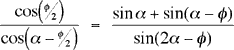
Cette identité figure rarement dans les manuels scolaires.
La spirale logarithmique.
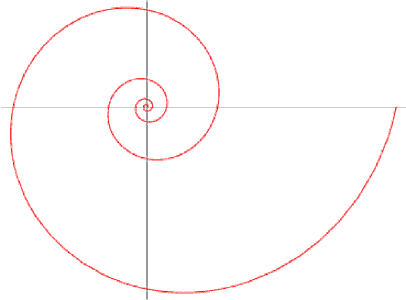
En laissant tendre l'angle entre les rayons successifs vers zéro, on obtient la spirale logarithmique dont l'équation en coordonnées polaires est r = ecot(α) θ. Cette courbe intersecte chaque rayon (infiniment souvent) a un angle α. Le site
dont est tiré la figure, contient plus d'information (en anglais) sur la spirale logarithmique. Le bouquin A Book of Curves par E.H. Lockwood (Cambridge University Press, 1971, Chapitre 9, pages 98-109) discute du paradoxe apparent de cette courbe "infinie" qui a une longueur finie. En fait, on peut considérer l'origine O comme la fin de la courbe. Le livre contient également une version "infinie" du premier diagramme de Hecquet.
Une autre généralisation
Szechtman divise le cercle en n parties égales et somme seulement la longueur des n premiers segments. Avec une mesure en radians on a donc φ = 2π/n (et α = π/2). En procédant comme dans la première solution, et en utilisant la formule de la somme d'une progression géométrique finie, on obtient une longueur desegment de
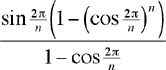
Lorsque n tend vers l'infini, l'angle x = 2π/n tend vers zéro, et la courbe s'approche du cercle. Donc en posant
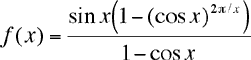
on doit s'attendre à voir f(x) tendre vers 2π lorsque x tend vers 0. C'est un exercice intéressant pour ceux qui connaissent la règle de l'Hôpital.