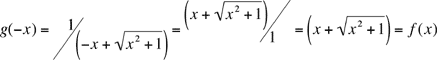Si les réels x et y vérifient l'équation

trouvez leur somme x + y.

Merci à Andy Liu de l'Université de l'Alberta pour ce problème du mois.

Solution au problème de mars 2005

Nous avons reçu des solutions correctes de

Tout le monde a trouvé la solution x + y = 0, de plusieurs façons différentes. Hecquet note qu'avec ce problème, "l'intérêt n'est pas tant dans sa résolution effective, mais plutôt dans la façon de le faire". Nous reproduisons ci-bas ses diverses rubriques, en notant ceux qui ont proposé une solution similaire.

Donc

et

en élevant au carré,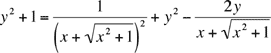

On sépare les variables

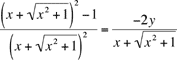
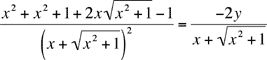
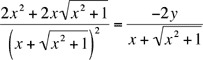
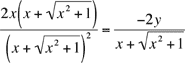
En simplifiant des deux côtés : x=-y, et donc x+y=0

2- Un peu plus fûté (La méthode de Amghibech, Barroso, et Moutaharir.)

En remarquant que

Si on multiple des deux côtés par :

Soit (E1)

De même, si on multiplie des deux côtés l'égalité initiale par :

Et donc (E2)

En réalisant (E1)+(E2) :

2(x+y) = 0, et donc x+y=0

3- A la Euler (La méthode de Cahangirov, Lo Presti, Loyer, Anonyme, et Tran.)

x et y étant des réels, sachant que la fonction sinh (sinus hyperbolique) est un bijection de R sur R, il est possible de trouver 2 rééls u et v tels que sinh(u)=x et sinh(v)=y.

L'équation devient donc

Or cosh²(u) - sinh²(u)=1, donc 1 + sinh²(u)=cosh²(u).
De plus, la fonction cosh est strictement positive sur R, donc

Donc, dans l'équation initiale:
(sinh(u)+cosh(u))(sinh(v)+cosh(v))=1
Or, sinh(u)+cosh(u)=exp(u) (car sinh(u)=(exp(u)-exp(-u))/2 et cosh(u)=(exp(u)+exp(-u))/2 )
Donc, exp(u).exp(v)=1, exp(u+v)=1
Donc u+v=0. Donc u=-v. Or, sinh(-v)=-sinh(v),
et donc sinh(u)=-sinh(v) => x=-y et x+y=0.

(Note: l'essentiel de cette méthode est d'isoler x dans l'expression , puis y dans , ce qu'on peut faire sans fonctions hyperboliques.)

4- Euler bis (La méthode de Arnaiz, Carpentier and Lichtenberg.)

Prenons le logarithme népérien de l'équation:

Donc,
Or (fonction réciproque de sinh établissant elle aussi une bijection de R sur R.) Donc Argsh(x)=-Argsh(y)=Argsh(-y) (sinh étant impaire, Argsh aussi), et comme Argsh est bijective, x = -y, donc x+y=0

5- Appel à l'âne à Lise (La méthode de Bornsztein)

Soit f la fonction qui à x associe , et g celle qui à x associe

Une étude rapide des fonctions montre que f est croissante, g décroissante, et surtout qu'elles sont toutes deux bijectives de R dans R⁺. Donc, f(x)=g(y) => g(-x)=g(y) => x=-y => x+y=0

6- A la Euclide

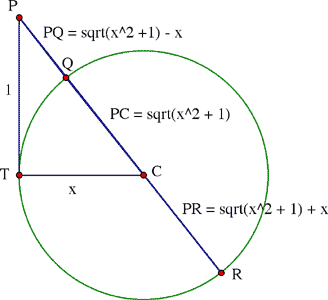
Cette approche est propre a Hecquet, qui a donné le début d'un argument graphique. Nous l'avons modifié un peu, et nous "laissons au lecteur le soin de compléter les détails" (comme on dit quand on ne sait pas trop quoi faire). Notre dessin se base sur deux propositions du livre 3 des éléments d'Euclide:

1. (Proposition 36) Soit un cercle et P un point extérieur au cercle. Si de P on laisse tomber une tangente au cercle touchant celui-ci à T, et une sécante au cercle touchant celui-ci à Q et R, alors le rectangle de dimensions PQ et PR a la même aire que le carré de côté PT.

et

2. (Proposition 18) Soit une tangente à un cercle. Alors le rayon le rayon joignant le centre du cercle au point de contact est perpendiculaire à la tangente.

La figure qui suit montre le triangle rectangle PTC de base x, de hauteur 1 et d'hypothénuse .

Problèmes et solutions précédents