Le double-zapping
Ce mois-ci, nous montrons comment on peut se servir de la télévision à des fins éducatives. Supposons que vous ayez deux télévisions côte à côte, une rouge et une bleue, ayant chacune sa télécommande. Vous n'utiliserez que deux boutons sur chaque télécommande, soit le bouton + qui permet de passer à la chaîne suivante et le bouton - qui permet de passer à la chaîne précédente. Nous appelerons double-zapping l'action de peser simultanément sur un bouton de la télécommande rouge et sur un bouton de la télécommande bleue, de façon à changer de chaîne sur les deux télévisions en même temps. Ainsi, de (Chaîne 8, Chaîne 6), on peut double-zapper à (Chaîne 7, Chaîne 5), (Chaîne 7, Chaîne 7), (Chaîne 9, Chaîne 5) ou (Chaîne 9, Chaîne 7).
Pour le problème du mois, on suppose que vous avez TROIS télévisions côte à côte, chacune avec sa propre télécommande, et connectées à trois compagnies de câble différentes:
La télévision A est connectée à la compagnie Alpha offrant 70 chaînes (notées A1 a A70),
la télévision B est connectée à la compagnie Beta offrant 60 chaînes (B1 a B60) et
la télévision C est connectée à la compagnie Gamma offrant 94 chaînes (C1 a C94).
Vous réalisez cependant que les compagnies offrant plus de chaînes n'offrent pas plus de choix: Les trois compagnies diffusent exactement les mêmes réseaux, et il y a beaucoup de répétitions. En particulier, les chaînes A1, B1 et C1 sont identiques, et les chaînes A70, B60 et C94 sont identiques. Puis, à la longue, vous réalisez qu'il est possible de double-zapper de (A1,B1) à (A70,B60) de telle sorte que l'émission diffusée sur la télévision A soit toujours la même que celle diffusée sur la télévision B; et de même, qu'il est possible de double-zapper de (B1,C1) à (B60,C94) de telle sorte que l'émission diffusée sur la télévision B soit toujours la même que celle diffusée sur la télévision C.
Le problème de février: Dans ces conditions, est-il nécéssairement possible de double-zapper de (A1,C1) à (A70,C94) de telle sorte que l'émission diffusée sur la télévision A soit toujours la même que celle diffusée sur la télévision C?
MISE EN GARDE: Il ne faut pas peser sur le bouton - lorsque l'appareil de télévision est à la chaîne 1, ni peser sur le bouton + lorsque l'appareil est à la dernière chaîne. Cela ferait exploser la télévision et invaliderait votre police d'assurance.
Solution au problème MP48
Oui, il est toujours possible de double-zapper de (A1, C1) à (A70, C94) de telle sorte que la télévision A montre toujours la même émission que celle diffusée sur la télévision C. En fait on peut même triple-zapper de (A1,B1,C1) à (A70,B60,C94) (si on a le pied suffisamment agile).
Nous avons reçu une solution partielle de Xavier Hecquet (France), qui indique que le problème est plus facile à résoudre lorsque toutes les chaînes de B montrent des émissions différentes. Dans ce cas, on peut passer de (A1,B1) à (A70,B60) sans jamais presser le bouton - sur la télécommande de A. En effet, si on passe de (Ai,Bj) à (Ai+1,Bj') puis à (Ai,Bj''), alors j = j'' (puisque toutes les chaînes de B sont différentes), donc ces deux étapes s'annulent. Nous allons d'abord résoudre le problème lorsque toutes les chaînes de B sont différentes.
Solution 1: Toutes les chaînes de B correspondent à des réseaux différents.
On construit un graphe G dont les sommets sont les couples (Ai,Ck) correspondant au même Bj, où (Ai,Bj) est relié par une arète à (Ai',Cj') si on peut double-zapper de l'un à l'autre.
La table ci-haut correspond à un plus petit exemple où la télévision B a trois chaînes et les télévisions A et C en ont 9 chacune. Le graphe G défini ci-haut est alors le suivant:
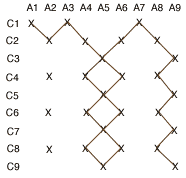
Ce graphe contient des sommets isolés comme (A2,C6), et le long chemin (A1,C1), (A2,C2), (A3,C1), (A4,C2), (A5,C3), (A6,C2), (A7,C1), (A8,C2), (A9,C3), (A8,C4), (A9,C5), (A8,C6), (A9,C7), (A8,C8), (A9,C9). Nous démontrerons que G contient nécessairement un tel chemin des premières aux dernières chaînes de A et C, en se servant de la propriété locale suivante:
Lemme 1: Si A et C ont respectivement m et n chaînes, alors (A1,C1) et (Am,Cn) ont un chacun un voisin, et les autres sommets de G ont chacun un nombre pair de voisins.
Démonstration: Supposons que (Ai,Ck) correspond à la chaîne Bj, où 1 < i < m et i < k < n. Puisqu'on peut double-zapper de (A1,B1) à (Am,Bt) (où t est le nombre de chaînes de B), les chaîne Ai+1 et Ai-1 correspondent chacune à une des chaînes Bj-1, Bj+1. De même, puisqu'on peut double-zapper de (B1,C1) à (Bt,Cn), les chaîne Ck+1 et Ck-1 correspondent chacune à une des chaînes Bj-1, Bj+1. Par exemple, Ai+1 pourrait correspondre à Bj-1, et Ai-1, Ck+1, Ck-1 pourraient correspondre à Bj+1, et alors (Ai,Ck) aurait (Ai-1,Ck-1) et (Ai-1,Ck+1) pour voisins. Il y a en tout seize possibilités, énumérées dans le tableau suivant.
| Voisins de
(Ai,Ck) | Ck-1 = Bj-1
Ck+1 = Bj-1 |
Ck-1 = Bj-1
Ck+1 = Bj+1 |
Ck-1 = Bj+1
Ck+1 = Bj-1 |
Ck-1 = Bj+1
Ck+1 = Bj+1 |
| Ai-1 = Bj-1
Ai+1 = Bj-1 |
(Ai-1,Ck-1)
(Ai-1,Ck+1) (Ai+1,Ck-1) (Ai+1,Ck+1) |
(Ai-1,Ck-1)
(Ai+1,Ck-1) |
(Ai-1,Ck+1)
(Ai+1,Ck+1) |
|
| Ai-1 = Bj-1
Ai+1 = Bj+1 |
(Ai-1,Ck-1)
(Ai-1,Ck+1) |
(Ai-1,Ck-1)
(Ai+1,Ck+1) |
(Ai-1,Ck+1)
(Ai+1,Ck-1) |
(Ai+1,Ck-1)
(Ai+1,Ck+1) |
| Ai-1 = Bj+1
Ai+1 = Bj-1 |
(Ai+1,Ck-1)
(Ai+1,Ck+1) |
(Ai-1,Ck+1)
(Ai+1,Ck-1) |
(Ai-1,Ck-1)
(Ai+1,Ck+1) |
(Ai-1,Ck-1)
(Ai-1,Ck+1) |
| Ai-1 = Bj+1
Ai+1 = Bj+1 |
(Ai-1,Ck+1)
(Ai+1,Ck+1) |
(Ai-1,Ck-1)
(Ai+1,Ck-1) |
(Ai-1,Ck-1)
(Ai-1,Ck+1) (Ai+1,Ck-1) (Ai+1,Ck+1) |
On doit aussi tenir compte des exceptions aux frontières, lorsque i = 1 ou m, ou k = 1 ou n. Lorsque 1 < k < n, et (A1,Ck) est un sommet du graphe, alors A1 = B1 = Ck, donc A2 = B2 = Ck-1 = Ck+1, donc (A1,Ck) a deux voisins (A2,Ck-1) et (A2,Ck+1). De même les sommets de la forme (Am,Ck), 1 < k < m, (Ai,C1) ou (Ai,Cn), 1 < i < m ont chacun deux voisins. Les deux sommets (A1,C1) et (Am,Cn) ont chacun un voisin, et (A1,Cn), (Am,C1) n'appartiennent pas au graphe puisque A1 = B1, Cn = Bt, Am = Bt et C1 = B1. Ainsi le lemme est démontré.
Le nombre de voisins d'un sommet d'un graphe est appelé le "degré" de ce sommet. Ainsi le lemme precedent dit que tous les sommets du graphe G ont un degré pair, sauf (A1,C1) et (Am,Cn) qui ont degré 1. Un des premiers résultats de la théorie des graphes est le suivant:
Lemme 2: Tout graphe a un nombre pair de sommets de degré impair.
Démonstration: Lorsqu'on additionne les degrés de tous les sommets, on obtient le double du nombre d'arètes, puisqu'on a compté chaque arète deux fois. Ce résultat étant pair, le nombre de termes pairs de la somme devait donc être pair. C'est tout!
Ce lemme confirme ce qu'on sait de G, qui a exactement deux sommets de degré impair, soit (A1,C1) et (Am,Cn). Peut-on en déduire plus? Oui! Il s'agit d'appliquer le Lemme 2 à un plus petit graphe H qui contient les sommets de G qu'on peut atteindre à partir de (A1,C1) avec une série de double-zaps. Ainsi, H contient (A1,C1), et lorsqu'un sommet (Ai,Ck) de G est dans H, alors tous ses voisins le sont également. Le degré de tout sommet de H est donc le même que son degré dans G. H contient le sommet (A1,C1) de degré impair, et selon le Lemme 2, H doit contenir au moins un autre sommet de degré impair. Mais le seul candidat est (Am,Cn), qui appartient donc à H. Ainsi, il est possible de se déplacer de (A1,C1) à (Am,Cn) avec une série de double-zaps.
Cette démonstration n'est pas valide lorsque les chaînes sur B sont répétées. Par exemple si dans l'exemle précédent on remplace tous les 3 par des 1, alors il faut ajouter plusieurs sommets à G, dont (A1,C9) qui aura degré 1. Nous verrons ci-bas comment adapter la démonstration au cas général.
Solution 2: Le cas général.
On appelle "cohérent" un double-zap de deux chaînes identiques à deux chaînes identiques. L'énoncé général est le suivant:
Si les télévisions A, B et C on respectivement m, t et n chaînes, et si il existe des séries de double-zaps cohérents de (A1,B1) à (Am,Bt) et de (B1,C1) à (Bt,Cn), alors il existe une série de double-zaps cohérents de (A1,C1) à (Am,Cn).
Démonstration: Soit P = {(A1,B1), (A2,B2), (Ai3,Bi3), (Ai4,Bi4), ..., (Am-1,Bt-1), (Am,Bt) }, une chemin correspondant à une série de double-zaps cohérents de (A1,B1) à (Am,Bt) aussi courte que possible. Alors la même chaîne Ai peut être la première coordonnée de plusieurs couples de P, et la même chaîne Bj peut être la deuxième coordonnée de plusieurs couples de P, mais le même couple (Ai,Bj) ne peut apparaître deux fois dans P, autrement il serait possible de raccourcir P. De même, soit Q = {(B1,C1), (B2,C2), (Bj3,Cj3), ..., (Bt-1,Cn-1), (Bt,Cn)}, un chemin correspondant à une série de double-zaps cohérents de (B1,C1) à (Bt,Cn) aussi courte que possible. On définit le graphe G dont les sommets sont les triplets (Ai,Bj,Ck) tels que (Ai,Bj) est dans P et (Bj,Ck) est dans Q, où (Ai,Bj,Ck) est adjacent à (Ai',Bj',Ck') lorsque dans P, (Ai,Bj) et (Ai',Bj') sont adjacents, et dans Q, (Bj,Ck) et (Bj',Ck') sont adjacents.
Comme dans la première solution, nous démontrerons que (A1,B1,C1) et (An,Bt,Cm) sont les seuls sommets de degré impair dans G, ce qui impliqu'il existe une série de triple-zaps cohérents de (A1,B1,C1) à (Am,Bt,Cm). En laissant tomber la télécommande de B, on en tire une série de triple-zaps cohérents de (A1,C1) à (Am,Cn).
Lemme 3: Tous les sommets de G ont degré pair, sauf (A1,B1,C1) et (Am,Bt,Cn) qui ont degré 1.
Démonstration du Lemme 3: Soit (Ai,Bj,Ck), un sommet de G. En général, (Ai,Bj) a deux voisins (Ai',Bj'), (Ai'',Bj'') dans P, et (Bj,Ck) a deux voisins (Bj''',Ck'), (Bj'''',Ck'') dans Q. Chacun de i' et i'' est alors i-1 ou i+1, et de même chacun de j', j'', j''', j'''' est j-1 ou j+1 et chacun de k', k'' est k-1 ou k+1. En particulier j', j'', j''' et j'''' prennent en tout au plus deux valeurs, donc il y a égalité entre certains de ces termes. Les voisins de (Ai,Bj,Ck) correspondent aux égalités entre d'une part j' ou j'' et d'autre part j''' ou j''''; par exemple, si j'' = j''', alors (Ai'',Bj'',Ck') est voisin de (Ai,Bj,Ck). Or puisque j', j'', j''' et j'''' prennent au plus deux valeurs, il y a un nombre pair de ces égalités, donc (Ai,Bj,Ck) a un nombre pair de voisins. On voit facilement que les sommets de frontière de type (A1,B1,Ck), (Am,Bt,Ck), (Ai, B1,C1) et (Ai,Bt,Cn) sont tous de degré 2, sauf (A1,B1,C1) et (Am,Bt,Cn) qui sont de degré 1. Le lemme est ainsi démontré, ce qui complète la solution.
Problèmes et solutions
précédents