Les longueurs des côtés consécutifs d'un quadrilatère sont 6, 33, 47 et 34. Quel est l'angle entre ses diagonales?

(Malgré les apparences, ces longueurs n'ont pas été choisies au hasard.)

Nous avons reçu des solutions correctes de

Mehdi Abdeh-Kolahchi (Halifax)		Xavier Hecquet (France)
Theerasak Asawanonwiwat (Thailande)		Eric Hsiung (États Unis)
Bernard Carpentier (France)		Normand LaLiberté (Ontario)
K.A. Chandrashekara (.com)		Arne Loosveldt (.com)
Pablo de la Viuda (Espagne)		Patrick LoPresti (États Unis)
H.N. Gupta (Regina)		Wolfgang Kais (Allemagne)

Réponse:

L’angle entre les deux diagonales est 90º.

            Nous savons tous que lorsque les longueurs des côtés d’un triangle sont prescrites, sa forme est déterminée.  Par contre, la forme du quadrangle ABCD n’est pas déterminée par les longueurs  6, 33, 47, 34 de ses côtés: Si on construit un quadrilatère avec des bâtonnets de longueurs p, q, r, s, avec des joints souples aux sommets, on peut le déformer comme le quadrilatère de Figure 1.  (Vous pouvez déplacer le point C sans changer les longueurs p, q, r, s.)  Les longueurs p, q, r, s de la Figure 1

Sorry, this page requires a Java-compatible web browser.
Figure 1

ont été choisies telles que p + s = q + r, ce qui implique que l’angle entre AC et BD n’est pas constant — on peut voir qu’il décroît vers zéro lorsque A et C s’approchent de la diagonale  BD.  Il est donc surprenant qu’on puisse spécifier les longueurs de telle sorte que AC demeure perpendiculaire à BD dans toutes les positions (comme dans la Figure 2 où le point peut être déplacé, de même que les longueurs du quadrangle auxiliaire). 

Sorry, this page requires a Java-compatible web browser. Figure 2

En fait, dans sa solution, Chandrashekara a simplement fait référence au théorème de Peaucellier:

Les sommes des carrés des côtés opposés d’un quadrilatère sont égales si
et seulement si les diagonales sont perpendiculaires

Dans notre quadrilatère, p = 6, q = 33, r = 47, et s = 34, donc 

p² + r² = 6² + 47² = 2245 = 33² + 34² = q² + s². 

Nous discuterons de l’importance et de l’histoire de ce théorème à la fin. Nous présentons d’abord quatre démonstrations de notre problème. En remplaçant les nombres 6, 33, 47, 34 par p, q, r, s, on obtient une démonstration générale avec chaque approche.

1.  Démonstration avec coordonnées. (La méthode de Hecquet et Kais.)

Nous allons modifier la solution de Hecquet en plaçant l’origine au point B et en positionnant D à un point (k, 0) sur l’axe des x.  Ainsi le point A sera un des deux points d’intersection du cercle de centre B et de rayon 33 et du cercle de centre D et de rayon 6.  Ainsi les coordonnées (x,y) de A sont sujettes aux contraintes
x² + y² = 33² = 189 et (x - k)² + y² = 6² = 36.

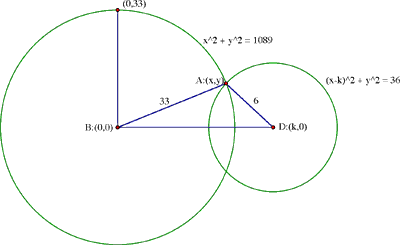
Figure 3

En soustrayant la deuxième équation de la première, on trouve 2kx – k² = 1053, donc la première coordonnée de A satisfait

Également, les coordonnées (x, y) de C satisfont

x² + y² = 47² = 2209 et (x - k)² + y² = 34² = 1156.

En soustrayant la deuxième équation de la première, on découvre que la première coordonnée de C est la même que celle de A. Ainsi, A et C sont sur une même droite verticale, et AC est perpendiculaire a BD.

2.  Démonstration avec la loi du cosinus. (la méthode de Abdeh-Kolahchi, Asawanonwiwat, Carpentier, Chandrashekara, de la Viuda, LaLiberté, Loosveldt, et LoPresti). 

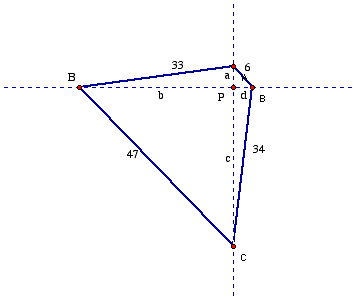
Nous allons présenter une combinaison des arguments de Abdeh-Kolahchi, de la Viuda, et LoPresti.  Soit P, le point d’intersection de AC et BD (étiquetés comme dans la Figure 2).  Notons a, b, c, d les distances respectives de P à A, B, C et D (dans cet ordre), et q l’angle APB.  On a cos q = –cos(180º – q).  On appliqué la loi du cosinus successivement aux triangles APB, BPC, CPD, et DPA,

332 = a2 + b2 – 2ab cos q,             472 = b2 + c2 + 2bc cos q,             342 = c2 + d2 – 2cd cos q,              62 = d2 + a2 + 2da cos q.

En soustrayant la première équation et la troisième de la somme des deux autres, on obtient

47² + 6² –33² – 34² = 2(ab + bc + cd + da) cos q

Sachant que le terme de gauche est 2245 – 2245 = 0,  il suffit de démontrer que 2(ab + bc + cd + da) est positif pour conclure que cos q = 0, donc q = 90º.  On a ab + bc + cd + da = (a + c)(b + d) = AC·BD, où a, b, c, d sont les distances à P. Ainsi, l’équation a + c = 0, impliquerait A = C = P; mais A et C ne peuvent pas tous les deux être sur le segment BD, puisque 33 + 6 ≠ 47 + 34.  De la même façon, b + d ≠ 0, donc le produit de ces deux termes est non-nul, ce qui complète la démonstration.

3.  Démonstration avec le Théorème de Pythagore.  (La méthode de Gupta, Hsiung et de Carpentier  pour sa deuxième démonstration.)

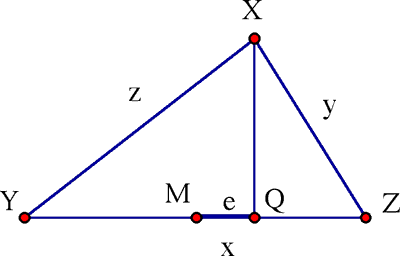
Figure 4

Lemme. Dans tout triangle XYZ dont les côtés  satisfont z ≥ y, l’altitude à X intersecte le côté opposé  YZ en un point Q dont la distance au point milieu est

Proof. Pythagore nous dit que XQ² = YX² – YQ² = ZX² – ZQ², donc 

En développant et simplifiant, on obtient z² – y² = 2xe, donc e = ( z² – y²)/2x tel qu’annoncé. 

On applique ce lemme aux triangles ABD et CBD.  Dans la Figure 2 ci-haut, DABD est au dessus, et z = 33, y = 6,  X = BD, donc 

Au dessous, on a DCBD où z = 47, y = 34, et x = BD, donc

a la même valeur.  Donc les perpendiculaires de A et C à BD touchent ce segment à la même distance de son point milieu. Puisqu’il n’existe qu’une seule perpendiculaire à BD de ce point, cette perpendiculaire doit être la droite AC. Par conséquent AC est perpendiculaire à BD.

4. Démonstration avec le produit scalaire. (La troisième solution de Carpentier)

Notons PQ le vecteur du point P au point Q (en particulier QP = -PQ).  Avec la notation de la figure de la deuxième démonstration, Carpentier note qu’il suffit de démontrer que le produit scalaire AC · DB est nul, et en présente un développement amusant :

AC · DB = ½[AC · (DB + DB)]

= ½[AC · (DC + CB + DA + AB)]

= ½[AC · (AB + CB) + AC · (DC + DA)]

= ½[(AB + BC) · (AB - BC) + (AD + DC) · (DC - AD)]

= ½[ AB · AB - BC · BC + CD · DC - AD · AD]

= ½[33² – 47² + 34² – 6²]

= 0.

Notes Historiques

Charles-Nicolas Peaucellier (1832-1913) était capitaine de l’armée française en 1864 lorsqu’il inventa l’inverseur de Peaucellier ["... Cette découverte a été énoncée en termes généraux, et sous forme de question dans les Nouvelles Annales mathématiques, page 414; son exposition détaillée est parue dans le même journal en 1873, page 71."].  Cet inverseur de Peaucellier est un appareil pour dessiner l’inverse de toute courbe, qui fut la première solution mécanique au problème de transformer un mouvement circulaire en mouvement rectilinéaire: dans la Figure 5, lorsque D trace un cercle à travers B, D' se déplace sur une droite perpendiculaire au diamètre de ce cercle passant par B. Cet appareil est constitué de deux tiges de longueur r et deux de longueur s, jointes aux B et C du quadrilatère ADCD' en forme de cerf-volant, avec des tiges plus longues de longueur p et q reliant les coins A et C à un pivot fixe à B. Selon le théorème de Peaucellier,

Sorry, this page requires a Java-compatible web browser.
figure 5

p² – s² = b² – d² = (b – d)·(b + d) = BD·BD'.

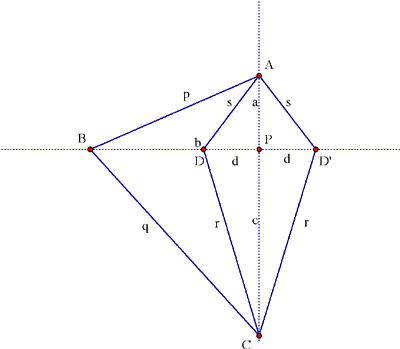
Figure 6

En supposant que p² – s² = q² – r² (ce qui correspond à la perpendicularité de AC et BD lorsque les long côtés p et q sont issus du même sommet) le produit BD·BD' est constant lorsque les longueurs p, q, r, et s sont fixes.  Par définition ceci veut dire que D' est l’inverse du point D dans un cercle dont le centre est B et le rayon  .  Ainsi, lorsqu’on trace avec le point D les courbes d’une figure donnée, un crayon à D’ trace la figure inverse. En ajoutant une septième tige et un pivot pour maintenir D sur un cercle passant par B, D’ tracera une ligne droite. Les livres de géométrie traitant de l’inversion (comme Introduction to Geometry de H.S.M. Coxeter, Chapitre 6), parlent de cette histoire, tout comme les livres portant de la géométrie des nombres complexes (sous l’appellation de transformations linéaires ou de Möbius). On peut aussi consulter les pages

http://mathworld.wolfram.com/Inversion.html et http://www.cut-the-knot.org/pythagoras/invert.shtml.

Google peut aussi trouver d’autre pages portant sur ce sujet.  Nous avons trouve certaines informations historiques au site
http://sunsite.utk.edu/math_archives/.http/hypermail/historia/feb99/0014.html.  (Nous ne les avons pas confirmées.)  Nos informations au sujet du théorème de Peaucellier proviennent de Exercices de géométrie, 4ème édition (1907), par F. G.-M, pages 505, 506, et 513.