Les quatres points A, B, C, D sont situés dans l'espace de telle sorte que toute sphère ayant A et B sur sa surface intersecte toute sphère ayant C et D sur sa surface. Que peut-on dire de plus au sujet de ces quatre points?

Solution au problème MP35

Nous avons reçu une solution correcte de Patrick J. Lo Pesti (Etats Unis).
D'autres correspondants ont peut-être essayé de nous faire parvenir leurs
solutions, mais à cause de nos problèmes de courriel, nous ne les avons pas reçues.

On commence par démontrer la première assertion. La démontration de Lo Pesti consiste en trois affirmations.

Observation 1. Les droites AB et CD intersectent ou sont égales.
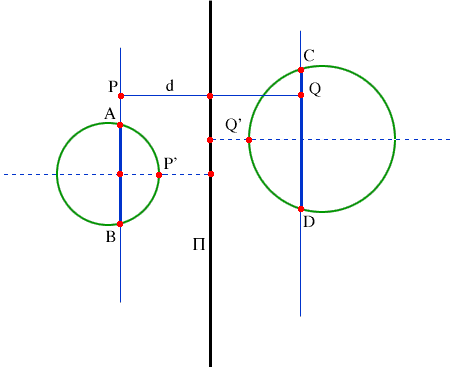
Démontration. Supposons le contraire, et notons d > 0 la distance minimale entre ces droites. Alors il existe un point P sur AB et un point Q sur CD tels que la distance de P à Q est d. Alors PQ est perpendiculaire à AB et CD. Soit ∏, le plan perpendiculaire au segment PQ à travers son point millieu. On choisit un point P' sur la médiatrice du segment AB perpendiculaire à ∏. Alors la sphère passant par A, B et P' a son centre sur cette médiatrice, et n'intersecte pas ∏. De même, si Q' est sur la médiatrice du segment CD perpendiculaire à ∏, alors la sphère passant par C, D et Q' a son centre sur cette médiatrice, et n'intersecte pas ∏. Ces deux sphèreres n'ont aucune intersection, contrairement à notre hypothèse. Ainsi, les droites AB et CD s'intersectent ou coïncident.

Remarque. Par suite à l'Observation 1, les points A, B, C et D sont coplanaires, et le problème relève de la géométrie planaire. Cette version planaire est étudiée en détail dans Geometry Revisited par H.S.M. Coxeter et S.L. Greitzer (Mathematical Association of America, New Math Library No. 19 (1967), Théorème 5.11 en page 104), et se base sur un problème du concours William Lowell Putnam de 1965.
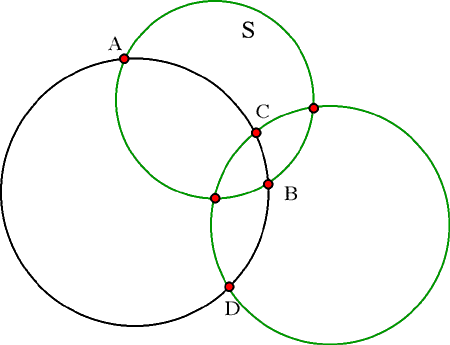
Observation 2. Les points A, B, C et D sont sur une droite ou un cercle.
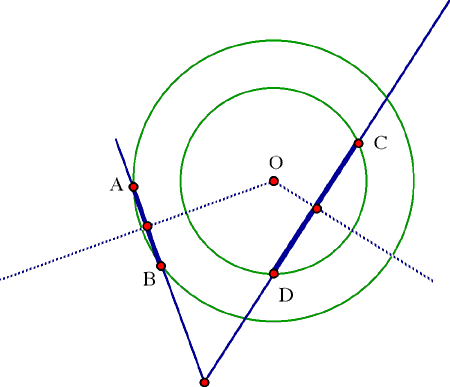
Démontration. Supposons que A, B, C et D ne sont pas colinéaires. Puisque les droites AB et CD se rencontrent, les médiatrices des segments AB et CD doivent aussi se rencontrer. Notons O le point de rencontre de ces deux médiatrices. Alors la sphère de centre O passant par A et B ne peut pas avoir un rayon différent de celle de centre O passant par C et D, car autrement on aurait là deux sphères disjointes passant par A, B et C, D respectivement, contrairement à notre hypothèse. Par conséquent, A, B, C et D sont sur un même cercle.

Observation 3. Les paires A, B et C, D se séparent mutuellement. (Par là on entend, sans perte de généralité, qu'on rencontre sucessivement les points A, C, B et D en parcourant le cercle sur lequel ils reposent en sens horaire, ou la droite sur laquelle ils reposent d'un bout à l'autre.)
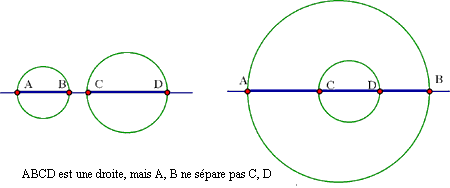
Démontration. Si les paires A, B et C, D sont colinéaires mais ne se séparent pas mutuellement, alors les sphères ayant AB et CD comme diamètres sont disjointes, contrairement à notre hypothèse.

Si A, B, C et D sont sur un cercle mais ne se séparent pas, alors poursuivant la construction de la démontration précédente, on choisit un point P' sur la médiatrice de AB, entre O et le point millieu de AB, et Q' sur la médiatrice de CD, entre O et le point millieu de CD. Alors les sphères déterminées respectivement par A, B, P', et par C, D, Q' sont situées de part et d'autre du plan déterminé par la droite perpendiculaire à ABCD passant par O, et le point de rencontre des droites AB et CD. Par conséquent, ces deux sphères sont disjointes, contrairement à notre hypothèse.

L'affirmation selon laquelle A, B, C et D sont sur une même droite ou sur un cercle, de telle sorte que les paires A, B et C, D se séparent mutuellement est donc démontrée. On démontre maintenant la réciproque.

Soit S, une sphère passant par A et B. Si S contient le cercle ABCD, alors clairement S intersecte toute sphère passant par C et D. Sinon, S sépare le cercle ou la droite ABCD de telle sorte que l'un des points C, D est à l'intérieur de S et l'autre à l'extérieur; par conséquent toute sphère passant par C et D doit rencontrer S.