Notre problème de février comporte deux parties:
-
Pour tout nombre n pair, montrez comment diviser un carré en n triangles d'aires égales.
-
Démontrez qu'il est impossible de diviser un carré en 3 triangles d'aires égales.
Nous avons reçu des solutions complètes de Pierre Bornsztein (France), Gilles Feyrit (France), Wolfgang Kais (Allemagne), Juan Mir Pieras (Espagne), et Patrick LoPresti (Etats Unis). Leurs méthodes sont similaires et se combinent en une jolie solution.
Solution au problème MP39
Solution à la première partie.
Il y a plusieurs façons de diviser un triangle en un nombre pair de triangles d'aires égales, tel qu'illustré dans la figure suivante de Mir. Nous verrons encore plus de solutions plus bas.
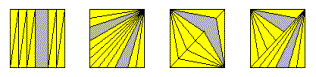
Solution à la deuxième partie.
Nous voulons séparer un triangle en trois triangles, ce que nous appellerons une 3-dissection. Toutes les solutions soumises montraient plus que ce qu'il est nécessaire:
Théorème. Dans toute 3-dissection d'un carré, l'aire d'un des carré est égale à la moitié de l'aire du carré original.
En fait, ce théorème implique le résultat souhaité — les aires des trois triangles ne peuvent pas être égales. On commence avec quelques observations préliminaires communes à plusieurs des solutions soumises:Démonstration du théorème.
Si les trois sommets d'un des triangles de la 3-dissection sont des sommets du carré, l'aire de ce triangle est la moitié de celle du carré. Sinon, les trois triangles doivent avoir le cinquième point pour sommet. Ce cinquième point est alors sur un côté du carré, et doit former avec le côté opposé un des triangles de la 3-dissection. L'aire de ce triangle est alors la moitié de celle du carré.
Observation 1. Les sommets des triangles de toute 3-dissection d'un carré forment un ensemble de 5 points, soit les quatre sommets du carré et un sommet qui est soit sur un côté du carré ou un côté d'un des autres triangles.
Démonstration. Les angles des triangles valent ensemble 3?180?. En comptant les angles du carré on obtient 2?180?. Le 180? qui reste correspond à un autre point, qui doit se trouver sur un côté du carré ou d'un triangle.
Observation 2. Tout triangle d'une 3-dissection a au moins deux sommets en commun avec le carré.
Démonstration. C'est une conséquence immédiate de la première observation, puisqu'un point seulement n'est pas sommet du carré.
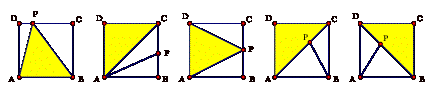
Les trois configurations possibles des cinq points et de la 3-dissection sont données dans la figure ci-haut.
Commentaires sur les extensions du problème.
Peut-on partager un carré en 5, 7, ou en un nombre impair arbitraire de triangles d'aires égales? Mir n'a pas essayé de répondre à cette question, mais il a demontré que si le carré peut être partagé en n triangles d'aires égales, il peut aussi être partagé en n+4 triangles d'aires égales, tel qu'illustré dans la figure suivante.

Les courbes en noir sont des quarts de cercles dont le rayon est la moitié du côté du carré, centrés sur les points millieux des côtés du carré. Selon une proposition d'Euclide, tout angle inscrit dans un demi cercle est droit. Ainsi les quatre triangles en bleu sont des triangles rectangles, laissant au centre un carré bleu. En ajustant les proportions il est donc possible de complémenter une dissection du carré bleu en n triangles pour obtenir une dissection du carré rouge en n+4 triangles rectangles. On obtient ainsi des dissections originales de carrés en un nombre pair de triangles rectangles. S'il était possible de dissecter un triangle rectangle en un nombre impair n de triangles on pourrait utiliser cette construction pour obtenir des dissections en n + 4k triangles pour tout k.
Le problème de la dissection d'un carré en un nombre impair de triangles d'aires égales semble d'abord avoir été soulevé par Fred Richman en 1965. Son collègue John Thomas y a répondu en partie; Paul Monsky (American Mathematical Monthly 77:2 (fevrier 1970), 161-164), poursuivant le travail, a démontré que la réponse est
Il n'existe pas de dissection d'un carré en un nombre impair de triangles d'aires égales.
La démonstration n'est ni élémentaire, ni très compliquée. Sherman Stein raconte son histoire dans un article paru, par coincidence, le mois dernier: “Cutting a Polygon into Triangles of Equal Areas,” The Mathematical Intelligencer, 26:1 (2004), 17-21. Stein y parle aussi de questions similaires au sujet des dissections de toute sortes de solides en plusieurs dimensions. Certains de ces problèmes ne sont toujours pas résolus. Merci à Pierre Bornsztein de nous avoir communiqué cette référence.
Problèmes et solutions
précédents