(a) Soit une collection de points dans le plan telle que
- La distance entre n'importe quels deux points est un nombre
entier
- une infinité de ces points sont colinéaires.
(b) Qu'arrive-t-il si on demande seulement que 5 points soient colinéaires?
Pierre Bornsztein (de Pontoise, France), Steve Brooke (de Vancouver), Juan Mir Pieras (d'Espagne) et Jacob Tsimerman (de Toronto) nous ont envoyés leurs solutions.
Deux démonstrations de (a).
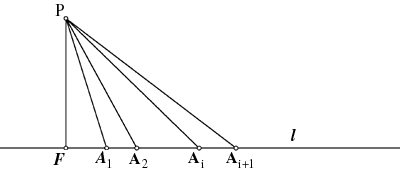
Soit S, l'ensemble de points donné, et l, la ligne qui
contient une infinité de points de S. Supposons qu'il existe un point
P de S qui n'est pas sur l, et notons F le point d'intersection
de l avec la perpendiculaire à l qui passe par P. D'un côté
ou l'autre de F, la droite l doit contenir une infinité de points
de S. Notons ces points successivement A1, A2, ... à mesure que l'on
s'éloigne de F. Puisque PAi est un entier positif pour tout i,
PAi+1 >= PAi + 1. Conséquemment, la distance PAi croît sans bornes
lorsque i croît vers l'infini. On utilise un résultat préliminaire
de Bornsztein:
Les distances FAi sont toutes rationnelles.
En effet, on note que
| PA22 | = | PF2 + FA22 |
| = | PF2 + (FA1 + A1A2)2 | |
| = | PF2 + FA12 + 2(FA1)(A1A2) + A1A22 | |
| = | PA12 + 2(FA1)(A1A2) + A1A22 |
Mis à part FA1, toutes ces distances sont entières, et on a
soit un nombre rationnel.
On peut maintenant modifier la configuration pour transformer ces distances rationnelles en distances entières: On dilate la configuration par un facteur de 2A1A2; alors toutes les distances sont multipliées par 2A1A2, donc celles qui étaient entières le demeurent, et toutes les distances FAi le deviennent. On peut donc supposer sans perte de généralité que toutes les distances FAi et PAi sont entières dès le départ.
La solution de Bornsztein repose sur ces observations:
Puisque PAi et FAi sont respectivement l'hypothénuse
et le côté d'un triangle rectangle, on a PAi - FAi > = 1.
Par suite,
| PF2 | = | PAi2 - FAi2 |
| = | (PAi + FAi)(PAi - FAi) | |
| >= | (PAi + FAi) | |
| >= | PAi |
Par conséquent, si P était un point de S qui n'est pas sur l, alors les distances PAi seraient bornées par PF2 (le carré de la distance de P à F), ce qui contredit le fait que ces distances ne sont pas bornées. Anisi, le point P ne peut pas exister, ce qui complète notre première démonstration.
En fait, nos observations préliminaires indiquent que l'on peut démontrer que pour tout nombre positif d, il existe seulement un nombre fini de triangles rectangles dont l'hypothénuse et un côté sont entiers, alors que l'autre côté est de longueur d.
Voici la démonstration suggérée par Brooke et fournie par Tsimerman:
Soit d = PF et x = FAi, où Ai est sur la ligne l. On démontre que
si i est assez grand alors ![]() n'est
pas un nombre entier. En effet, on a PAi > FAi; s'il s'agit de
deux nombres entiers, alors PAi >= FAi + 1, donc
PAi2 >= (FAi + 1)2 = FAi2 + 2FAi + 1.
Avec PAi2 = d2 + FAi2, cela implique d2 >= 2FAi + 1,
soit FAi <= (d2 - 1)/2. Lorsque i est grand, cette borne
n'est pas respectée (puisque les distances FAi croissent à l'infini),
donc PAi et FAi ne peuvent pas être toutes deux entières.
n'est
pas un nombre entier. En effet, on a PAi > FAi; s'il s'agit de
deux nombres entiers, alors PAi >= FAi + 1, donc
PAi2 >= (FAi + 1)2 = FAi2 + 2FAi + 1.
Avec PAi2 = d2 + FAi2, cela implique d2 >= 2FAi + 1,
soit FAi <= (d2 - 1)/2. Lorsque i est grand, cette borne
n'est pas respectée (puisque les distances FAi croissent à l'infini),
donc PAi et FAi ne peuvent pas être toutes deux entières.
Réponse à (b).
Bornsztein, Mir et Tsimerman donne l'ensemble S = { (0,12), (-16,0), (-9,0), (0,0), (9,0), (16,0) }, comme exemple d'ensemble contenant cinq points colinéaires, où toutes les distances sont entières. Cet exemple est construit à partir du triplet de Pythagore (4,3,5), donnant les dimensions d'un triangle rectangle dont les deux côtés et l'hypothénuse sont entiers. Le plus petit commun multiple des côtés est 12, et on place les points (0,0) et (0,12). Il existe alors quatre façons d'ajouter un point sur l'abscisse pour compléter un triangle similaire au triangle original, ce qui nous donne les quatre autres points de S. Mir nous indique la généralisation: A partir de k triplets de Pythagore (A1,b1,c1), (A2, b2, c2), ..., (ak, bk, ck) (où Ai2 + bi2 = ci2 pour i = 1, ..., k), on peut construire un ensemble S de 4k+2 points, dont 4k+1 sont colinéaires. Par exemple, avec les triplets (4,3,5) et (12,5,13), on trouve le plus petit commun multiple des côtés 3, 4, 5 et 12, qui est 60, et on place dans S les points (0,60), (0,0), ainsi que les points (-144,0), (-80,0), (-45,0), (-25,0), (25,0), (45,0), (80,0), (144,0), qui chacun forme avec les deux premiers points un triangle de dimensions proportionnelles au triangle 4,3,5 ou au triangle 12,5,13. Cette construction se généralise à un nombre arbitraire de triplets de Pythagore. Or, puisqu'il existe une infinité de triplets de Pythagore de la forme (2mn, m2-n2, m2+n2), On peut former un ensemble S avec autant de points qu'on veut sur une même ligne, pourvu que ce nombre ne soit pas infini.
Brooke nous réfère au site http://mathworld.wolfram.com qui donne plusieurs informations intéressantes sur les triplets de Pythagore (en anglais avec les mot-clefs "Pythagorean triples"). Pour sa part, Bornsztein nous indique la généralisation due à Anning et Erdšs: Si S est un ensemble infini de points du plan tel où toutes les distances sont entières, alors tous les points sont colinéaires. A ce sujet, on peut consulter H. Hadwiger, H. Debrunner, and V. Klee, Combinatorial Geometry in the Plane. Holt, Reinhart, and Wilson, (1964), Problème 2-9.