On a 3 = 1 + 2, 5 = 2 + 3, 6 = 1 + 2 + 3, 7 = 3 + 4, mais ni 4 ni 8
ne peuvent s'écrire comme somme d'au moins deux entiers consécutifs. Votre mission est de démontrer que ce motif se poursuit à l'infini:

1. Démontrez qu'aucune puissance de 2 ne peut s'écrire comme somme
   d'au moins deux entiers consécutifs.
   
   
2. Démontrez que tout entier qui n'est pas une puissance de 2 peut
   s'écrire comme somme d'au moins deux entiers consécutifs.

Solution au problème MP30

Ce mois-ci, nous avons eu la réponse d'un comité formé de Francesco Barioli (de Regina), Pierre Bornsztein (de France), Normand Laliberté  (d'Ontario), Juan Mir Pieras (d'Espagne), Alexander Potapenko (de Russie), Jason Stein (de Regina), et Philippe Thenoz. Bornsztein  et Potapenko ont démontré un résultat plus général sur le nombre de solutions possibles. Les autres donnaient des arguments similaires qui pourraient être généralisés de la même façon.  Nous reproduisons ici la solution de Bornsztein.

Nous allons prouver un résultat plus fort (voir théorème et corollaires ci-dessous). Dans tout ce qui suit, les nombres considérés sont des entiers strictement positifs.

Si n = a + (a+1) + ... + (a+r-1) = r(2a+r-1)/2, où a > 0 est un entier, on dira que n admet une décomposition d'ordre r. En particulier, puisque n = n, tout entier admet une décomposition d'ordre 1. De plus, si r est fixé, puisque la fonction a -> r(2a+r-1)/2 est strictement croissante sur {1,2,3,...}, un entier n donné admet au plus une décomposition d'ordre r.

On note R_i(n) le nombre de décompositions de n d'ordres impairs, R_p(n) le nombre de décompositions de n d'ordre paires, et R(n) = R_i(n) + R_p(n).

Théorème: Si n > 0 alors :

1. R_i(n) (resp. R_p(n) ) est égal au nombre de diviseurs de n impairs et positifs t tels que t(t+1)/2 ≤ n (resp. t(t+1)/2 > n)
2. R(n) = d(m), où n = m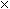2^k , avec m impair (et d(.) désigne le nombre de diviseurs strictement positifs).
   

Preuve:

1. Si n admet une décomposition d'ordre r impair, alors il existe un unique a > 0 tel que n = r(2a+r-1)/2, ainsi r est un diviseur positif impair de n.
   De plus, 2a+r-1 ≥ r+1, donc r(r+1)/2 ≤ n.
   
   Réciproquement, si r est un diviseur impair de n tel que r(r+1)/2 =< n.
   On pose a = n/r - (r-1)/2. On vérifie facilement que a > 0 est entier et qu'il fournit une décomposition de n d'ordre r, que l'on sait unique. Cela prouve l'affirmation sur R_i(n).
    
   Si n admet une décomposition d'ordre r pair. Alors, il existe un unique a > 0 tel que
   n =r(2a+r-1)/2. On pose t = 2a+r-1. Alors t > 0 entier impair et divise n.
   De plus, t(t+1) = t(2a+r) > tr = 2n, d'où t(t+1)/2 > n.
   
   Réciproquement, si t > 0 diviseur impair de n tel que t(t+1)/2 > n. On pose r = 2n/t et a = (t+1-r)/2, et on vérifie facilement que r > 0 est pair, a > 0 et que n = r(2a+r-1)/2, c'est à dire n admet une décomposition d'ordre r que l'on sait unique. Cela prouve le résultat sur R_p(n).
   
2. Il est clair qu'alors R(n) est la somme de tous les diviseurs impairs positifs de n, ce qui conduit à  la formule annoncée.
   

Corollaires:

1. Si n est une puissance de 2 alors R(n) = 1, et la seule décomposition de n est celle d'ordre 1 (d'où la réponse à  la première des questions posées pour le problème de Février).
   
2. Si n est premier impair, alors R(n) = 2. Comme, d'autre part, on a n = 2k+1 = k + (k+1), on en déduit que les seules décompositions de n sont celles d'ordre 1 et d'ordre 2.
   
3. Si n = m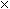2^k, avec k≥1 et m ≥ 3 impair, alors R(n) ≥ 2. Cela assure que n peut s'écrire comme une somme d'au moins deux entiers consécutifs, mais on a mieux : Puisque n est impair, il ne peut admettre de décomposition d'ordre 2 (un pair + un impair = un impair), et donc admet une décomposition d'ordre au moins 3.
   
4. Si n est impair composé, alors R(n) ≥ 3, et donc n admet une décomposition d'ordre au moins 3.
   
5. De b), c) et d), on déduit que tout entier qui n'est pas une puissance de 2 s'écrit comme une somme d'au moins deux entiers consécutifs (d'où la réponse à la question 2).
   
6. De a),b),c) et d), on déduit que les entiers qui ne peuvent pas s'écrire comme une somme d'au moins trois entiers consécutifs sont les puissances de 2 et les nombres premiers.
   

Remarques:

Si l'on veut en savoir plus sur le sujet, on peut prouver que :

1. (R(1) + R(2) + ... + R(n))/n = 0,5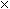Ln(n) + (2C + Ln(2) -1)/2 + O(1/rac(n)) où C est la constante d'Euler, rac désigne la racine carrée, et O est la notation "Grand O" (big O).
   
2. Si R(n,s) désigne le nombre de décompositions de n en une somme de termes consécutifs d'une suite arithmétique de raison s, alors :
   R(n,s) = 2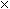d(m) pour s impair et n = m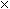2^k et m impair.
   R(n,s) = d(n) pour s pair.
   

Ces résultats sont (semble-t-il) dûs à  Leveque (1950).

Références: