Complétez la phrase suivante en écrivant sur chaque ligne un nombre décimal de un ou plusieurs chiffres.
Solution au problème MP28
Nous avons reçu des solutions de Neil Chatani (Californie), Pierre
Bornsztein (France), Juan Mir Pieras (Espagne), et Gordon Robinson (Colombie
Britannique). Il n'y a aucune relation entre notre correspondant Robinson
et Raphael M. Robinson (1911-1995) qui a composé le problème.
Celui-ci était un mathématicien versatile, qui a grandement
contribué à la réputation du département de
mathématiques de l'Université de Berkley. En plus de ses
travaux en logique, en théorie des nombres en en beaucoup d'autres
domaines, il s'est toujours intéressé aux mathématiques
recréatives, inventant et résolvant plusieurs problèmes
de divers niveaux de difficulté. Gordon Robinson a noté
que notre formulation du problème admet plusieurs interprétations.
Selon notre interprétation, les deux solutions correctes sont "Dans cette phrase, le nombre de 0 est 1,
de 1 est 7, de 2 est 3,
de 3 est 2, de 4 est 1,
de 5 est 1, de 6 est 1,
de 7 est 2, de 8 est 1
et de 9 est 1." et "Dans cette phrase, le nombre de 0 est 1,
de 1 est 11, de 2 est 2,
de 3 est 1, de 4 est 1,
de 5 est 1, de 6 est 1,
de 7 est 1, de 8 est 1
et de 9 est 1." Dans cette deuxième solution on compte deux fois le chiffre 1
dans le nombre 11, plutôt que de compter le nombre 11. Si on comptait
des nombres plutôt que des chiffres, on pourrait aussi admettre
la solution "Dans cette phrase, le nombre de 0 est 1, de 1 est 10, de 2 est 1, de
3 est 1, de 4 est 1, de 5 est 1, de 6 est 1, de 7 est 1, de 8 est 1 et
de 9 est 1.", où le "10" ne contribue ni au compte des "0", ni au compte des
"1". Pour préciser qu'on demande un compte de chiffres plutôt
que de nombres, il aurait été préférable d'écrire
la phrase comme suit: Dans cette phrase, le nombre de "0" est __, de "1" est __, de "2" est
__, de "3" est __, de "4" est __, de "5" est __, de "6" est __, de "7"
est __, de "8" est __ et de "9" est __. La première solution, où toutes les inconnues sont des
entiers, est la plus naturelle. On peut démontrer que c'est la
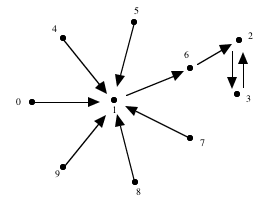
seule solution de ce genre en considérant le graphe obtenu en placant
une flèche de x à y si dans la phrase, le nombre de x est
y. Dans ce graphe, les chiffres avec des flèches pointant à
1 sont ceux vers lesquels aucune flèche ne pointe, et les chiffres
avec des flèches pointant à 2 sont ceux vers lesquels pointe
exactement une flèche. En général, il y a une flèche
de x à y si y est un plus le nombre de flèches qui pointent
à x. Examinons le chemin 1 -> x1 -> x2 ->
... commençant à 1. Puisqu'il y a un nombre fini de chiffres,
ce chemin doit créer un cycle lorsqu'un nouvel élément
xj pointe vers un élément xi déjà
rencontré. En fait, la composante qui contient 1 ne contient rien
d'autre que les que ce chemin et les chiffres pointant vers 1. En effet,
lorsqu'on quitte le cycle en parcourant les flèches à rebours,
on doit nécessairement terminer à un cul de sac, c'est à
dire un chiffre pointant vers 1. Notons qu'il y a au moins deux chiffres qui pointent vers 1: 0 et au
moins un des chiffres parmi 7, 8 et 9. Ainsi, 1 pointe vers un chiffre
x supérieur à 2. Tous les chiffres du chemin x -> y -> z
-> ... doivent ensuite pointer vers 2, sauf 2 lui-même; on a donc
x -> 2 -> 3 -> 2. Les autres chiffres de cette composante pointent tous
vers 1. En fait, on peut maintenant démontrer qu'il y a une seule
composante. En effet, dans chaque composante il y a exactement une flèche
sortant de chaque chiffre, donc en moyenne il y a une flèche pointant
vers chaque chiffre. Par conséquemment, chaque composante contient
un chiffre vers lequel au plus une flèche pointe, et ce chiffre
est de la composante de 1 et 2. Ainsi le graphe est connexe, et les six
autres chiffres pointent vers 1. La première solution se déduit
de ce graphe. On s'arrête brièvement pour donner une version de la phrase
de Robinson en chiffres romains: Présents dans cette phrase, on compte IX fois "I", I fois "V",
II fois "X", I fois "L", I fois "C", I fois "D" et I fois "M". Entre autres, ceci démontre que le nombre de façons de
compléter la phrase de Robinson dépend du système
de numération utilisé. La deuxième solution, comptant
vingt et un chiffres, fonctionne seulement en base 10. Son existence pose
cependant un problème: Existe-t-il d'autres solutions comportant
plus de chiffres? L'intuition dit qu'une solution ne peut pas compter
trop de chiffres, puisqu'en regroupant ces chiffres pour remplir un blanc,
on forme de plus gros chiffres que la solution devrait en compter au départ.
Formellement, si N dénote le nombre de chiffres dans une solution,
alors où k = N (mod 10) si N (mod 10)
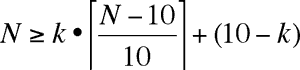
0, et k = 10 si N (mod 10) = 0. Cette identité est fausse déjà
pour N = 22, donc toute solution compte au plus vingt et un chiffres.
Dans notre page anglaise, Gordon Robinson démontre que la deuxième
solution est en fait la seule solution à vingt et un chiffres.
Centrale des Maths