Solution au problème de septembre:
Les détectives Juan Mir Pieras d'Espagne et Normand Laliberté d'Ontario ont clairement établi le fait suivant: Descartes est le coupable; il ment en prétendant avoir vu Abel.
Dans le diagramme suivant, chaque professeur est représenté
par son initiale. Chaque professeur est relié par une flèche
à chaque professeur qu'il prétend avoir vu. On sait que chaque
professeur est entré une seule fois, et quand deux professeurs se
trouvaient en même temps au salon, au moins un des deux a remarqué
l'autre.
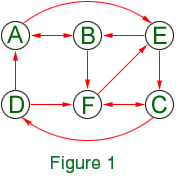
- Solution de Laliberté: Il est certain qu'Abel et Bernoulli se sont trouvés en même temps au salon: chacun prétend avoir vu l'autre, et au moins un des deux dit la vérité. De même, Il est certain que Cauchy et Fermat se sont trouvés en même temps au salon. Or, Abel et Cauchy ne se sont jamais trouvés en même temps au salon, puisqu'aucun des deux n'a remarqué l'autre (il en va de même pour Abel et Fermat). Donc, l'intervalle de temps AB ou Abel et Bernoulli étaient tous deux présents est disjoint de l'intervalle CF ou Cauchy et Fermat étaient tous deux présents. Nous allons supposer que AB a précédé CF (l'autre cas étant similaire).
- Solution de Mir: On dit qu'un contact visuel s'est établi entre deux professeurs lorsqu'ils se sont retrouvés en même temps au salon, et au moins un d'entre eux a remarqué l'autre. Il nous est donné une liste dix contacts visuels, dont neuf sont vrais et un est faux.
Maintenant, Abel prétend avoir vu Erdös, qui
prétend avoir vu Bernoulli, et Fermat prétend avoir vu Erdös
qui prétend avoir vu Cauchy. Donc, Erdös est arrivé au salon
avant que le dernier d'entre Abel et Bernoulli ne parte, et en est reparti
seulement après que le premier d'entre Cauchy et Fermat ne soit
entré.
Ainsi, les événements suivants se sont produits dans l'ordre: 1 - Bernoulli est entré, 2 - Abel est sorti, 3 - Le premier d'entre Cauchy et Fermat est entré, 4 - Erdös est sorti.
Maintenant, on démontre que Descartes est entré au salon seulement aprés ces événements. En effet, Cauchy prétend avoir vu Descartes, qui prétend avoir vu Fermat. Donc Descartes s'est trouvé dans la pièce en même temps que Cauchy ou Fermat, mais jamais en même temps que Bernoulli ou Erdös. Il n'a pas pu quitter la pièce avant que Bernoulli n'entre, donc il est entré après que Bernoulli soit sorti. Mais au moment ou Bernoulli quittait la pièce, ou Erdös était déja présent, ou Abel y était toujours, et dans ce dernier cas Erdös allait entrer avant qu'Abel ne quitte, soit avant que le premier d'entre Cauchy et Fermat n'entre. Descartes allait donc entrer seulement après la sortie d'Erdös, alors que Cauchy ou Fermat se trouvait toujours au salon.
Par conséquent, Descartes est entré seulement après qu'Abel ne soit sorti. Il ment lorsqu'il affirme avoir vu ce dernier.
Lorsque trois professeurs se trouvent en même
temps au salon, il en résulte nécessairement un ``triangle
visuel'', c'est à dire qu'un contact visuel existe entre chaque
paire de ces professeurs. Notre liste contient quatre triangles visuels:
Abel-Bernoulli-Erdös, Bernoulli-Erdös-Fermat, Cauchy-Descartes-Fermat et
Cauchy-Erdös-Fermat. En tout, ces triangles visuels contiennent neuf contacts
visuels.
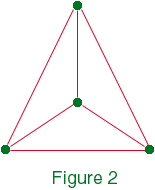
Si quatre professeurs s'étaient trouvés
en même temps au salon, il eût résulté un "tétraêdre
visuel" comme le suivant. Or notre liste de contacts visuels (qui ne comporte
aucune omission) ne contient aucun tétraêdre visuel. Par conséquent,
jamais plus de trois professeurs ne se sont trouvés ensemble au
salon.
Maintenant, on compte les contacts visuels en attribuant le crédit d'un contact au second de ses membres à entrer au salon (qui ne correspond pas nécessairement à celui qui a remarqué l'autre). En particulier, le premier professeur qui le matin est entré au salon n'a aucun contact visuel à son crédit, et le second en a au plus un. Les autres professeurs, du troisième au sixième, ont chacun au plus deux contacts visuels à leur crédit, puisque jamais quatre professeurs ne se sont trouvés en même temps au salon. Mais alors, la seule façon d'obtenir un total de neuf contacts visuels est d'avoir effectivement un contact au crédit du second professeur, et deux contacts au crédit de chaque professeur subséquent. Par conséquent, chaque professeur à partir du troisième a créé un triangle visuel en entrant au salon. Ainsi les quatres triangles visuels énumérés plus haut se sont effectivement produits. Le faux contact visuel est le seul qui n'est contenu dans aucun de ces triangles: Descartes a menti en prétendant avoir vu Abel.
Notes: Supposons que la période où chaque professeur s'est trouvé au salon est telle qu'indiquée dans la table suivante:
Abel: de 9:00 à 10:00 Bernoulli: de 9:20 à 10:40 Cauchy: de 11:00 à 12:00 Descartes: de 11:40 à 12:40 Erdös: de 9:40 à 11:20 Fermat: de 10:20 à 12:20
On illustre cette situation en représentant chaque
professeur par un point portant son initiale, et en reliant deux de ceux-ci
par une ligne lorsque les périodes où ils se trouvaient au
salon se chevauchent.
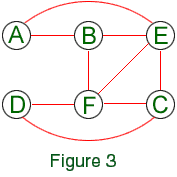
On obtient ce qu'on appelle un graphe d'intervalles: Les points correspondent à des intervalles (de temps) et deux d'entre eux sont reliés par une ligne lorsque les intervalles correspondants ont une partie commune.
Or le diagramme donné plus haut (faisant abstraction
des flèches) est obtenu de ce graphe en ajoutant une ligne entre
A et D. La solution du problème réside dans l'observation
que ce nouveau graphe n'est pas un graphe d'intervalle. En effet, la configuration
du 4-cycle induit illustrée ci-dessous est impossible dans les graphes
d'intervalles: Les intervalles W et Y n'ont aucune partie commune; si W
précède Y, alors X doit couvrir au moins tout l'intervalle
de la fin de W au début de Y, et il en va de même pour Z.
Ainsi, X et Z ont une partie commune et devraient être reliés
par une ligne.

Dans le diagramme donné plus haut, on trouve trois de ces 4-cycles induits: A-D-F-B, A-D-F-E et A-D-C-E. Le menteur se retrouve nécessairement dans chacun de ces 4-cycles, et de plus la supression de son (ou ses) mensonge(s) doit briser tous ces 4-cycles. La seule possibilité est donc celle mentionnée plus haut: Descartes a menti en prétendant avoir vu Abel.
L'idée d'utiliser les graphes d'intervalles dans les histoires policières est exploitée plus à fond dans le roman "Qui a tué le Duc de Densmore" de Claude Berge, (Bibliothèque Oulipienne No67). Nous avons tiré la version présentée ici de Introduction to Graph Theory par D. West; elle est originalement parue dans Algorithmic Graph Theory and Perfect graphs par M. C. Golumbic.
To return to the previous page use your browser's back button.