Nous avons reçu la solution suivante de Normand Laliberté (Ontario)
A montrer que la "probabilité que le caissier puisse remettre la monnaie à chacun" est de 1/5.
Le problème peut être reformulé ainsi:
Considérant le nombre total de permutations de n paires de $1-$2, combien parmi celles-ci sont telles que, si l'on balaie de gauche à droite, le nombre de $1 rencontrés n'est jamais inférieur au nombre de $2 rencontrés; nous appelons "succès" une telle permutation. Le balayage de gauche à droite correspond à l'arrivée des personnes, de la première à la dernière. Nous numérotons ces positions de 1 à 8. Toute autre permutation est appelée "échec".
Nous observons d'abord qu'un échec ne peut se produire qu'en position impaire, disons 2j+1 où 0 <= j <= n-1. En effet, supposons que 2k soit la position la plus à gauche où le nombre de $2 excède pour la première fois le nombre de $1. Nous avons:
- nombre de $2 - nombre de $1 = 1
- nombre de $2 + nombre de $1 = 2j
donc
- 2 nombre de $2 = 2j + 1
Ce qui est clairement impossible.
Définissons:
- P(n): le nombre de permutations de n paires de $1-$2.
- P(n) = (2n)! / (n! n!); ceci est un résultat classique.
- S(n): le nombre succès pour n paires de $1-$2.
- E(n): le nombre d'échecs pour n paires de $1-$2.
- E2(n): le nombre de permutations ayant un 2 en position 1 -pour n paires de $1-$2.
- E2(n) = P(n) / 2 = (2n)! / (2 n! n!); puisque la moitié des permutations commencent avec 2- l'autre moitié avec 1.
- EP(n, 2j+1): le nombre d'échecs en position 2j+1 -pour n paires de $1-$2, avec 0 < j <= n-1; 2j+1 est la position la plus à gauche où le nombre de $2 excède pour la première fois le nombre de $1.
Observons maintenant que
- EP(n, 2j+1) = S(j) E2(n-j); En d'autres mots, le nombre d'échecs en position 2j+1 est égal au produit du nombre de succès pour les i premières paires par le nombre de permutations ayant un 2 en position 1 pour les autres n-j paires de $1-$2.
Mais
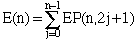. C'est-à-dire, le nombre total d'échecs est la somme des échecs en position 1, 3, 2n-1.
d'où
et donc -en remplaçant E2 et extrayant le facteur commun 1/2:
D'autre part:
- E(n) + S(n)= P(n); car une permutation est ou un échec ou un succès.
d'où
- S(n)= P(n) - E(n) (**)
Convenons que S(0)= 1 = P(0) - donc E(0) = 0.
Nous pouvons aisément vérifier que pour n = 1
S(1)= 1 = P(1) / 2 - donc E(1) = 1
En effet pour une paire $1-$2, il n'y a que 2 permutations:
- 12 (succès)
- 21 (échec)
Appliquant successivement les formules (*) et (**)ci-dessus, nous pouvons construire la table suivante
|
n |
P(n) |
E(n) |
S(n) |
|
0 |
1 |
0 |
1 |
|
1 |
2 |
1 |
1 |
|
2 |
6 |
4 |
2 |
|
3 |
20 |
15 |
5 |
|
4 |
70 |
56 |
14 |
|
5 |
252 |
210 |
42 |
|
6 |
924 |
792 |
132 |
On voit que pour S(4) / P(4) = 1/5. Ceci complète la solution proprement dite.
On voit aussi que pour 0 <= n <= 6,
- S(n) = P(n) / (n + 1).
Cependant, nous n'avons pu ni prouver ni réfuter cette égalité en général.
Note: Cette égalité est effectivement valide en général. Dans notre page espagnole, on considére une récurrence plus générale, considérant les cas où le caissier a au départ un certain nombre de pièces de un dollar. Dans notre page anglaise, toute récurrence est évitée en utilisant un principe de réflexion.