| |
Solution au problème de mai 2002
Ce problème est tiré de la cinquième compétition annuelle par
équipes organisée par la section centrale nord de la Math Association
of America, qui a eu lieu le 10 novembre 2001.
La partie fractionnaire F(r) d'un nombre r est définie comme suit:
F(r) = r - (le plus grand entier qui ne dépasse pas r).
Par exemple,
F(12.34) = 0.34, F( 11/2) = 1/2, F( 8/3) = 2/3,
F(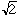 ) = 0.414213562...
Notre problème pour le mois de Mai:
Trouvez un nombre positif r tel que F(r) + F( 1/r) = 1. ) = 0.414213562...
Notre problème pour le mois de Mai:
Trouvez un nombre positif r tel que F(r) + F( 1/r) = 1.
Solution. Nous avons reçu des solutions correctes de
John Campbell (Edmonton, Alberta)
Normand Laliberté (Kitchener, Ontario)
Juan Mir Pieras (Espagne)
Alexander Potapenko (Russie)
Eulogio Ruiz-Sevilla (Espagne)
Tous ont donné une solution générale au problème de trouver
tous les nombres positifs r satisfaisant aux conditions
imposées. On présente une combinaison de leur cinq solutions.
On note d'abord que r ne vaut pas 1, parce que F(1) = F( 1/1) = 1.
On peut donc supposer que r > 1 et 0 < 1/r < 1.
Notre supposition F(r) + F(1/r) = 1 implique alors que
r + 1/r est un entier. Posons r + 1/r = n; on a alors
r 2 - nr + 1 = 0, d'où
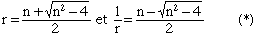 Réciproquement, pour tout entier n >= 3, on a
Réciproquement, pour tout entier n >= 3, on a
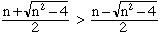 Puisque le produit de ces deux nombres est 1, on a
Puisque le produit de ces deux nombres est 1, on a
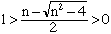 Ainsi
Ainsi
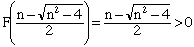 donc l'équation (*) donne une solution à
notre problème pour tout entier n >= 3. On doit exclure le cas n = 2
parce qu'il correspond à la solution fausse r = 1/r = 1. Ainsi
les deux plus petites solutions sont
n = 3:
donc l'équation (*) donne une solution à
notre problème pour tout entier n >= 3. On doit exclure le cas n = 2
parce qu'il correspond à la solution fausse r = 1/r = 1. Ainsi
les deux plus petites solutions sont
n = 3:
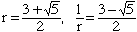 n = 4:
n = 4:
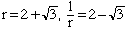 Commentaires sur le nombre d'or.
Commentaires sur le nombre d'or.
Même si tous nos correspondants ont répondu à la question
générale de caractériser toutes les solutions (ce qui est
plus intéressant et difficile), notons qu'il suffisait de trouver
seulement un nombre r tel que F(r) + F( 1/r) = 1.
C'eut été un exercice facile pour quiconque se souvient
des propriétés du nombre d'or. On utilise généralement
la lettre grecque 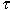 pour désigner le nombre d'or,
soit la racine positive de l'équation x 2 = x + 1.
On a donc pour désigner le nombre d'or,
soit la racine positive de l'équation x 2 = x + 1.
On a donc
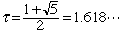 et l'équation
et l'équation
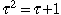 permet de calculer les puissances de permet de calculer les puissances de
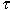 simplement avec des additions. Par exemple,
en multipliant les deux côtés par simplement avec des additions. Par exemple,
en multipliant les deux côtés par 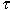 , on obtient , on obtient
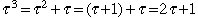 .
On peut aussi diviser les deux côtés par .
On peut aussi diviser les deux côtés par 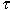 pour obtenir pour obtenir
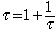 , soit , soit  . Après une seconde
division par . Après une seconde
division par 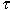 , cette équation devient , cette équation devient
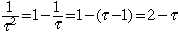 .
Ainsi, .
Ainsi, 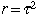 est une solution à notre problème original: est une solution à notre problème original:
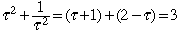 Il s'agit de la solution correspondant à n = 3 dans notre solution
générale.
Il s'agit de la solution correspondant à n = 3 dans notre solution
générale.
Problèmes et solutions précédents
Centrale des Maths
|
|