Votre ennemi choisit 2000 des nombres de 1 à 3000. Votre mission est de trouver 1000 nombres parmi ceux-là tels que leur parité alterne (pair, impair, pair, impair, ... ou l'inverse) lorsqu'on les classe du plus petit au plus grand.

Démontrez que vous pouvez toujours réussir, aussi futé que soit votre ennemi.

Nous remercions Aart Blokhuis de Technische Universiteit Eindhoven pour le problème de mars. Il l'a créé pour le Concours Mathématique de Hollande de l'année dernière. Nous avons reçu des solutions de

Toutes ces solutions sont très ingénieuses. Deux d'entre elles se ressemblent beaucoup, et les autres sont différentes. Il est très intéressant de les comparer.

Solution 1.Soumise par Francesco Barioli et indépendamment par Juan Mir Pieras.

Considérons les 1500 paires (1,2), (3,4), (5,6), ..., (2999, 3000). En choisissant 2000 nombres, notre ennemi a éliminé les 1000 nombres restant. Donc au plus 1000 des paires ci-haut peut contenir un (ou deux) de ces nombres éliminés. Ainsi il reste au moins 500 paires intactes, c'est à dire 500 paires dont les deux nombres ont été choisis par l'ennemi. On choisit simplement 500 de ces paires intactes, et on obtient une suite de 1000 nombres alternant entre impair et pair.

Solution 2.Soumise par Gordon Turpin.

La suite de nombres choisis par l'ennemi présenterait déjà une alternance impair-pair-impair-pair... si ce n'était des intervalles de nombres manquants. De ces intervalles de nombres manquants, on note que:

Seuls les intervalles contenant un nombre impair de nombres interrompent l'alternance de parité des nombres choisis.

Donc on peut choisir une suite alternée comme ceci: Si un nombre choisi par l'ennemi est précédé d'un intervalle impair de nombres manquants, alors on l'omet, mais autrement on l'inclut dans notre suite. La suite ainsi construite alterne entre nombres impairs et nombres pairs, et puisqu'il n'y a que 1000 nombres manquants, il y a au plus 1000 intervalles impairs de nombres manquants, et la suite que l'on construit contient au moins 2000 - 1000 = 1000 nombres.

Solution 3.Soumise par Alexander Potapenko.

On regarde encore les trous dans la suite choisie par l'ennemi, mais d'une autre façon. Notons x₁ x₂, ..., x₂₀₀₀ la suite choisie par l'ennemi, et posons x₁, x₂, ..., x₂₀₀₀,
y₁ = x₁ - 0, y₂ = x₂ - x₁, y₃ = x₃ - x₂, ..., y₂₀₀₀ = x₂₀₀₀ - x₁₉₉₉. Alors pour tout n on a

Pour ce faire, on définit Y_impair comme étant la moyenne de tous les nombres impairs de la suite des y, et Y_pair comme étant la moyenne de tous les nombres pairs de la suite des y. Évidemment, il de peut que la suite des y ne contienne que des nombres impairs (cas auquel Y_pair serait mal défini), mais alors on aurait a = 2000, ce qui résoudrait le problème.

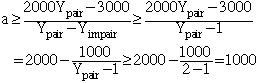
Solution 4. Soumise par Penny Nom.

Penny nous propose une variation de l'argument d'Alexander, démontrant qu'au moins 999 des différences y₂, y₃, ..., y₂₀₀₀ valent 1.
On a

Le reste du raisonnement va comme suit: Considérons la plus longue suite a₁, a₂, ..., a_p de parité alternée qu'on peut former avec les nombres choisis par l'ennemi. Alors les termes x_i qui viennent avant a₁ doivent avoir la même parité que a₁ (autrement il serait possible de rallonger la suite des a) et ainsi y_i+1 = x_i+1 - x_i est au moins 2. De même, les termes x_i qui viennent après a_p doivent avoir la même parité que a_p, de sorte que x_i - x_i-1 est au moins 2. De a_j à a_j+1, la parité des termes x_i ne peut changer qu'une seule fois (autrement il serait possible de rallonger la suite des a), donc entre a_j et a_j+1 il y a au plus un terme x_i - x_i-1 égal à 1. Ainsi, p - 1 vaut au moins 999, donc p est au moins 1000.