Les sept nains prennent leur petit déjeuner, et Blanche Neige leur a versé du lait. Avant de boire, les nains se livrent au rituel suivant: Le premier nain verse un sixième de son lait dans le verre de chacun de ses frères (ce qui le laisse avec rien du tout). Puis le deuxième nain fait la même chose, et ainsi de suite. Ce processus se poursuit autour de la table, jusqu'à ce que le septième nain aie distribué son lait de la même façon (il s'agit de Simplet). A la fin, chaque nain a dans son verre exactement la même quantité de lait qu'il avait au départ. Si Blanche Neige leur avait versé 42 onces de lait en tout, quelle quantité de lait chaque nain a-t-il reçu? Le problème a-t-il une seule solution, ou existe-t-il plusieurs solutions?
Ce problème est tiré du test d'application au camp mathématique Etats-Unis-Canada 2002.
Seulement six nains nous ont envoyé des solutions, soit John Campbell (Edmonton, Alberta), Normand Laliberté (Kitchener, Ontario), Juan Mir Pieras (Espagne), Penny Nom (Régina), Alexander Potapenko (Russie), et Gordon Robinson (Victoria, Colombie Britannique); chacun se mérite un verre de lait. Tous sont d'accord pour dire que les nains ont reçu respectivement
Maintenant, cette solution est-elle unique? Il est assez clair que le septième nain (Simplet) ne reçoit rien au départ (puisqu'il termine le processus en vidant son verre), mais il n'est pas aussi clair que la distribution du lait dans les autres verres doit nécessairement suivre une progression arithmétique 12, 10, 8, ... Les explications qui éclaircissent ce point se regroupent en trois catégorie:
Solution 1 (Potapenko, Robinson)Notons si la quantité de lait que le i-ième nain a reçu au départ, et ri la quantité de lait qu'il a reçu des autres nains avant de vider son verre. Le i-ième nain a si + ri onces dans son verre avant de vider en donnant (si + ri)/6 onces à chacun de ses frères. On a donc:
Or, si est aussi la quantité de lait qui se retrouve dans le verre du i-ième nain lorsque le processus se termine, c'est à dire la quantité qu'il reçoit des autres nains après avoir vidé son verre. On a donc:
Ces deux systèmes d'équations (12 équations en tout) permettent de déterminer les valeurs relatives de s1, s2, s3, ...: On sait que r1 = 0. Supposons s1 = 6. Alors l'équation (1) donne r2 = 1. Connaissant s1 et r2, l'équation (2) permet alors de trouver s2 = 5. Puis, connaissant s2 et r2, l'équation (1) permet de trouver r3 = 2, et ainsi de suite. Les valeurs si ainsi obtenues sont 6, 5, 4, 3, 2, 1 et 0. Mais puisque 6 + 5 + 4 + 3 + 2 + 1 + 0 = 21, il faut tout multiplier par 2 pour obtenir 42 onces de lait en tout. Ceci nous donne la distribution 12, 10, 8, ... qu'on a indiqué au départ comme unique solution au problème.
Solution 2 (Campbell, Mir)
On peut formuler les instructions algébriquement en termes des variables
si de la solution précédente. Soit S, le vecteur colonne dont les
entrées sont s1, s2, ..., s7 dans l'ordre. Alors le premier stage
du rituel correspond à la multiplication de S par la matrice
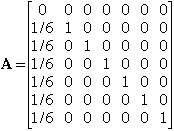
De même, les stages successifs correspondent à la multiplication par des matrices B, C, D, E, F, G, où la i-ième matrice a des 1 sur la diagonale sauf en i-ième position, des 1/6 dans la i-ième colonne sauf en i-ième position, et des 0 partout ailleurs. Notons P = GFEDCBA, la matrice qui représente le processus au complet. Le problème se réduit alors à démontrer que l'ensemble solution du système d'équations PS = S a dimension 1.
Il existe un résultat profond en algèbre linéaire, le théorème de Perron-Frobenius, qui permet de démontrer facilement le résultat souhaité. Cependant, comme il s'agit d'un thème avancé en algèbre linéaire, on laisse tomber cette approche. Cependant, l'expérience suivante qui est à la portée de nos lecteurs qui ont accès à un chiffrier, indique la puissance du théorème de Perron-Frobenius. Il nous a été suggéré par Robinson: Distribuons les 42 onces de lait arbitrairement entre les lutins, puis répétons le processus où chaque nain répartit son lait entre ses frères, pas seulement pour un cycle complet des 7 nains, mais pour plusieurs cycles. Algébriquement, ceci correspond à multiplier plusieurs fois le vecteur S par la matrice P. En fait, quelque soit la distribution originale des 42 onces, la distribution finale convergera rapidement vers la suite 12, 10, 8, 6, 4, 2, 0.
Solution 3 (Penny Nom)Si on abandonne provisoirement la condition s1 + s2 + ... + s7 = 42, l'ensemble des vecteurs (s1, s2, ..., s7) qui satisfont aux conditions de notre problème est un espace vectoriel, soit un ensemble clos sous les sommes, différences et multiplications par un scalaire. Ceci est une conséquence de l'approche matricielle de la solution 2 (pour ceux que cette approche rebute, on donne ci-bas une démonstration physique, en remplaçant le lait par de l'huile et de l'eau). On utilise aussi le fait que les valeurs s1, s2, ..., s7 sont toutes positives ou nulles.
On sait donc qu'avec s1 = 12, s2 = 10, ..., s7 = 0, les nains peuvent se livrer à leur rituel matinal et terminer avec la même quantité de lait qu'ils avaient au départ. Supposons donc que s1 = x1, s2 = x2, ... , s7 = x7 est une autre solution avec la même propriété. On a alors x7 = 0, et en multipliant par une constante appropriée, on peut supposer que x1 <= 12, x2 <= 10, x3 <= 8, x4 <= 6, x5 <= 4 et x6 <= 2, et qu'au moins une de ces contraintes est satisfaite avec égalité. Par soustraction, on obtient alors la nouvelle solution s1 = 12 - x1, s2 = 10 - x2, ..., s6 = 2 - x6 et s7 = 0. Ici, on a si = 0 pour au moins un des termes si autre que s7. Mais si un des lutins autre que Simplet se retrouve avec un verre vide après que Simplet aie vidé son verre, c'est que Simplet lui-même n'avait rien reçu des autres lutins, donc tous les verres étaient vides au départ. Ainsi, s1 = 12 - x1 = 0, donc x1 = 12, s2 = 10 - x2 = 0 donc x2 = 0, et ainsi de suite. Pour une quantité totale de 42 onces de lait, la solution s1 = 12, s2 = 10, ..., s7 = 0 est bien unique.
On termine en démontrant que si le rituel des lutins préserve les quantités originales s1 = 12, s2 = 10, ..., s7 = 0 et aussi les quantités s1 = x1, s2 = x2, ... , s7 = x7 alors le rituel préservera les quantités s1 = 12 - x1, s2 = 10 - x2, ..., s6 = 2 - x6 et s7 = 0 sans avoir recours au notions d'équations linéaires et d'espaces vectoriels. Pour ce faire on remplace le lait par de l'eau et de l'huile: Le premier lutin reçoit x1 onces d'eau et 12 - x1 onces d'huile, le deuxième x2 onces d'eau et 12 - x2 onces d'huile, et ainsi de suite. L'eau et l'huile ne se mélangent pas, donc chaque lutin doit prendre soin de bien brasser son verre avant d'en partager le contenu entre ses frères. A la fin du rituel, chaque lutin a la même quantité totale de liquide qu'il avait au départ, comme si c'était du lait. Si on laisse reposer le liquide un moment, alors l'eau et l'huile se séparent, et les lutins retrouvent respectivement x1, x2, ..., x7 onces d'eau dans leurs verres, comme au départ. Ainsi, les quantités respectives d'huile dans chaque verre, soit 12 - x1, 10 - x2, ..., 2 - x6, et 0 onces, sont également les mêmes qu'au départ.