Considérons le problème de placer le plus grand triangle équilatéral possible dans un triangle quelquonque T de côtés a, b et c (où a >= b >= c). Notons A, B et C respectivement les angles opposés à a, b et c. Il n'est pas difficile de démontrer que lorsque B mesure au plus 60 degrés, le plus grand triangle équilatéral repose sur le côté de longueur a. Lorsque B > 60, le plus grand triangle équilatéral repose parfois sur le côté de longueur c, dépendant d'une relation entre a, c et B à paraître dans "Equilateral Triangles in Triangles", un article de Richard P. Jerrard et John E. Wetzel dans le journal AMERICAN MATHEMATICAL MONTHLY.

Notre problème:

Quel est le seul triangle non-équilatéral tel que les trois plus grands triangles équilatéraux reposant respectivement sur les trois côtés sont égaux?

Juan Mir Pieras (d'Espagne), Boting Yang (de Régina) et Gordon Robinson (Victoria) nous ont envoyé des solutions correctes. En fait, Mir nous a envoyé trois solutions. La première se base sur la trigonométrie, la deuxième est plus géométrique, et la troisième est basée sur les triangles similaires. On donne ici la solution géométrique, combinée avec celle de Yang; les deux autres solutions se trouvent sur notre page espagnole.

Solution.

On note T le triangle ABC, et on note ses côtés a = BC, b = AC et c = AB. On peut supposer que a >= b >= c. Il nous est dit que les plus grands triangles équilatéraux basé sur a, b et c respectivement ont la même taille.

On montre d'abord que a = b. Le commentaire d'introduction au problème que le plus grand triangle équilatéral repose sur le plus grand ou le plus petit côté; la seule façon d'avoir un plus grand triangle équilatéral sur le côté b est d'avoir b = a ou b = c. Par contre, on élimine rapidement l'alternative ou b = c:

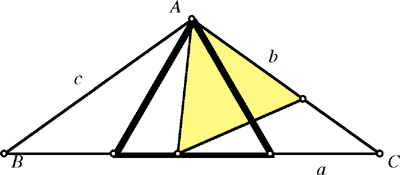
Un triangle isocèle dont les côtés les plus courts sont égaux

Si les côtés b et c étaient égaux (plus courts que a), alors le triangle équilatéral sur le côté a serait plus grand que tout triangle équilatéral sur b (comme dans la figure). la seule possibilité qui reste est que les deux côtés les plus longs soient égaux, c'est à dire a = b.

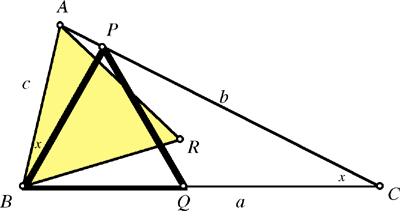
Un triangle isocèle dont les côtés les plus longs sont égaux

Puisque T est isocèle avec a = b, les angles A et B sont égaux et supérieurs à 60 degrés. Par conséquent le plus grand triangle équilatéral sur le côté a contient le point B. Soit BQP le plus grand triangle équilatéral sur a (avec P sur B) et ABR le plus grand triangle équilatéral sur c. Ces deux triangles sont égaux, donc BA = BP. Ainsi, le triangle ABP est isocéle. Et puisque ABP a l'angle en B en commun avec ABC, les triangles ABC et ABP sont similaires. Eb particulier, l'angle BAP est égal à l'angle BCA. Donc dans le triangle original, les angles en A B et C sont liés par la formule A = B = C + 60. Avec l'identité A + B + C = 180 degrés, on obtient A = 80 degrés, B = 80 degrés et C = 20 degrés.