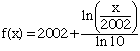| |
Solution au problème de janvier 2002
Pour tout nombre réel r, soit Tr, l'auto-application du plan
définie par
Tr(x,y) = (10r x, y+r).
Trouvez l'équation de la courbe continue y = f(x) qui contient
l'image du point (2002,2002) par toutes les applications Tr.
Solution
Ce mois ci nous avons reçu des solutions de Normand Laliberté
(Ontario), Juan Mir Pieras (Espagne), Alexander Potapenko (Russie),
Eulogio Ruiz González (Espagne) et Alex Wright (l'internet).
Toutes ces solutions étaient essentiellement la même,
les principales différences résidant dans la notation.
Nous allons noter log x le logarithme en base dix de x.
Ainsi, log(10r) = r.
On nous dit que Tr(2002,2002) = (10r(2002),2002 + r).
Donc pour tout r,
x = 10r(2002)
y = 2002 + r
En prenant le logarithme des deux côtés de la première égalité,
on obtient
log x = r + log 2002.
On peut donc éliminer le paramètre r de la deuxième équation
en lui substituant log x - log 2002. On obtient
y = f(x) = log x + 2002 - log 2002.
On a donc $f(x) 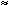 log x + 1998.7, puisque log 2002 log x + 1998.7, puisque log 2002 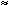 3.3.
En termes du logarithme naturel (base e), on peut aussi noter 3.3.
En termes du logarithme naturel (base e), on peut aussi noter
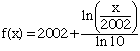
|
|