Un tétraèdre régulier est une pyramide dont les faces sont
quatre triangles équilatéraux, dont chaque paire a un côté
commun. Par conséquent, les six côtés ont la même longueur.
Imaginons que sur chaque face du tétraèdre, une voiture se
promène dans le sens des aiguilles d'une montre à vitesse
constante sur les côtés bordant cette face. Chacune des quatre
voitures a sa propre vitesse, et peut partir de n'importe quel
point de son parcours. Peut-on choisir ces paramêtres de sorte qu'aucune
collision ne se produise, ou est-il inévitable qu'une collision se
produise à un moment donné?
Nous avons reçu des solutions semblables de Juan Mir Pieras (Espagne) et Alexander Potapenko (Russie). On commence avec la solution de Potapenko.
Déjà, avec trois voitures, il y aura forcément une collision. Notons A, B, C, D les sommets du tétraèdre. Appelons GAUCHE la voiture parcourant le trajet ABC, DROITE la voiture parcourant le trajet ADB et BAS la voiture parcourant le trajet BDC.
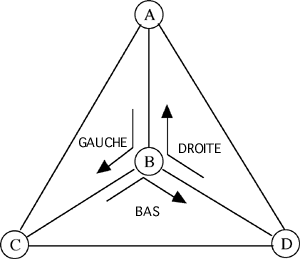
Une de ces trois voitures sera la plus lente. (Si il y en a plus d'une, on peut choisir n'importe laquelle.) Supposons que BAS est la plus lente, et considérons le moment où elle est située à B, se dirigeant vers D.
Où est alors DROITE? Si elle est sur l'arête DB, alors la collision avec BAS est inévitable. De même si elle est sur l'arête AD, alors Droite va atteindre le point D au plus tard en même temps que BAS, et encore une fois la collision entre ces deux voitures est inévitable. La seule possibilité qui reste est d'avoir DROITE sur l'arête BA.
Par un raisonnement similaire, on peut démontrer que puisqu'il n'y a pas eu de collisions entre BAS et GAUCHE, alors GAUCHE est sur l'arête AB. La façon la plus simple de le voir est d'avoir filmé toute la scène jusqu'au moment où BAS atteint le point B, et de la faire jouer à l'envers, en remontant dans le temps.
Ainsi, les voitures GAUCHE et DROITE sont toutes deux sur l'arête AB. Si il n'y a pas déjà eu de collisions entre elles, alors elles se dirigent l'une vers l'autre, et la collision est inévitable.
Commentaires.Malgré l'argument ci-haut, un avocat zèlé pourrait rétorquer qu'il existe une façon d'éviter les collisions: Il suffit de stipuler que la vitesse de chaque voiture est zéro. ça semble être une bonne façon de régler tous les problèmes de circulation: forcer tout le monde à laisser sa voiture stationnée en tout temps. En fait nos deux répondants nous ont suggéré des fa\{c}cons (plus réalistes) d'éviter les collisions:
Potapenko note que si deux des voitures, par exemple GAUCHE et DROITE se déplacent en sens horaire et les deux autres en sens antihoraire, alors il est facile déviter les collisions avec la règle suivante: Toutes les voitures ont la même vitesse, et pour deux voitures voyageant dans le même sens, lorsqu'une est au millieu de l'arête commune, l'autre est sur le sommet opposé.
Avec des modèles explicites, Mir note qu'il est possible de trouver des solutions où les voitures se rencontrent seulement aux sommets du tétraèdre. (Ainsi le réseau peut devenir sécuritaire en élargissant la route seulement à ces sommets.) Par exemple avec trois voitures à la même vitesse et une à la moitié de cette vitesse, on obtient la solution suivante (où les arêtes sont numérotées comme dans la figure):
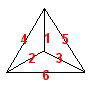
| GAUCHE | ... | 1 | 2 | 4 | 1 | 2 | 4 | ... |
| DROITE | ... | 5 | 3 | 1 | 5 | 3 | 1 | ... |
| BAS | ... | 3 | 6 | 2 | 3 | 6 | 2 | ... |
| ARRIÈRE | ... | 4 | 4 | 6 | 6 | 5 | 5 | ... |
Une autre solution est possible avec une voiture rapide et les trois autres voyageant à la moitié de sa vitesse, mais aucune autre combinaison n'est possible.
Ce problème est le problème hebdomadaire numéro 130 de la page de Alberto Delgado de l'Université Bradley (Peoria, IL): http://bradley.bradley.edu/~delgado/potw/potw.html
Ce problème lui a été suggéré par son collègue Tony Bedenikovic. Le professeur Delgado donne le commentaire suivant: