Un problème du concours danois "Georg Mohr Konkurrencen I Matematik 1996" a été généralisé par Pierre Bornsztein [CRUX MATHEMATICORUM 2001, page 240]. Il démontre que si
p est une permutation de l'ensemble {1, 2, ..., n} où n est congru à 2 ou 3 modulo 4, alors les nombres |k - p(k)| ne peuvent pas tous être différents. Ce mois-ci, on demande ce qui arrive lorsque n = 20:
Solution:
Juan Mir Pieras (d'Espagne) nous a envoyé une très jolie solution
qui ne règle pas seulement le cas n = 20, mais aussi tous les cas où n
est congru à 0 ou 1 modulo 4: Lorsque n = 4m, on construit la permutation
| Valeur de k | Valeur de p(k) | Valeur de |k - p(k)| |
|---|---|---|
| 1 <= k <= m | 4m + 1 - k | nombres impairs de 2m+1 à 4m-1 |
| k = m + 1 | m + 1 | 0 |
| m+1 < k <= 2m | 4m + 2 - k | nombres pairs de 2 à 2m-2 |
| 2m < k < 3m | 4m + 1 - k | nombres impairs de 1 à 2m-3 |
| 3m <= k | 4m - k | nombres pairs de 2m à 4m-2 |
| k = 4m | 2m + 1 | 2m - 1 |
Pour m=5, on a la solution à notre problème:
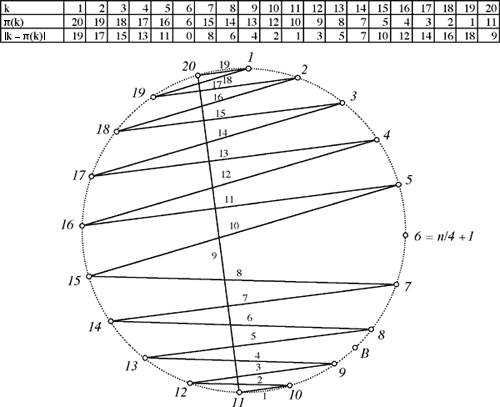
(Gordon Robinson note qu'il y a plusieurs solutions.)
Le cas n = 4m+1 est similaire:
| Valeur de k | Valeur de p(k) | Valeur de |k - p(k)| |
|---|---|---|
| 1 <= k <= m | 4m + 2 - k | nombres pairs de 2m+2 à 4m |
| k = m + 1 | m + 1 | 0 |
| m+1 < k <= 2m + 1 | 4m + 3 - k | nombres impairs de 1 à 2m-1 |
| 2m + 1 < k <= 3m | 4m + 2 - k | nombres pairs de 2 à 2m-2 |
| 3m < k <= 4m | 4m + 1 - k | nombres impairs de 2m+1 à 4m-1 |
| k = 4m + 1 | 2m + 1 | 2m |
Par exemple, pour m=2, n=9, on a
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| p(k) | 9 | 8 | 3 | 7 | 6 | 4 | 2 | 1 | 5 |
| D(k) = |k - p(k)| | 8 | 6 | 0 | 3 | 1 | 2 | 5 | 7 | 4 |
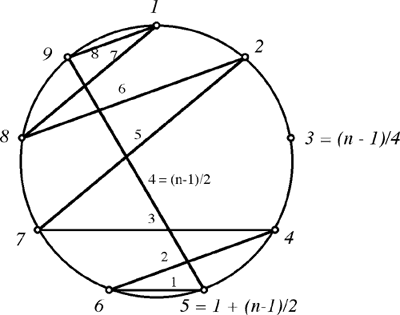
La solution générale se termine ici. Mir note aussi qu'il y a plusieurs autres solutions. En premier lieu, on doit tenir compte des symétries: si p est une permutation de l'ensemble {1,2,...,n} telle que les valeurs |k-p(k)| sont toutes différentes, alors il en va de même pour les permutations Q, R et S données par Q(k) = p-1(k), R(k) = n+1 - p(n+1-k) et S(k) = n+1 - Q(n+1-k). Ces quatre permutations sont toutes différentes. Ainsi, Pour n congru à 0 où 1 modulo 4, le nombre de permutations qui satisfont à la condition de notre problème est un multiple de 4.
Mir a calculé le nombre exact de ces permutations pour les petites valeurs de n:
| n | nombre de permutations distinctes | n | nombre de permutations distinctes |
|---|---|---|---|
| 4 | 4 x 1 | 5 | 4 x 1 |
| 8 | 4 x 8 | 9 | 4 x 24 |
| 12 | 4 x 248 | 13 | 4 x 628 |
| 16 | 4 x 12628 | 17 | 4 x 36036 |
On voit que le nombre de solutions augmente rapidement. Par contre pour n congru à 2 où 3 modulo 4, le nombre de solutions est zéro. On reproduit ici l'argument de Bornsztein paru dans CRUX MATHEMATICORUM (Gordon Robinson nous a envoyé un argument similaire).
Supposons que p est une permutation de {1, 2, ..., n} telle que
|k - p(k)| prend chacune des valeurs 0, 1, ..., n-1 exactement
une fois. Alors d'une part
et d'autre part
(puisque chaque nombre de 1 à n est additionné une fois et soustrait une fois). Combinant ces deux identités, on obtient
Or, pour tout nombre entier j, |j| + j est pair. Ainsi, le résultat n(n-1)/2 de la dernière sommation est pair. Par conséquent, n(n-1) est un multiple de 4, donc n ou n-1 est un multiple de 4.
Crux with Mayhem, publié la Société Mathématique du Canada, contient beaucoup de problèmes de ce genre. Pour plus d'information, consultez le site http://journals.cms.math.ca/CRUX/.