Pour célébrer l'arrivée du printemps, notre problème du mois rend hommage à la cuisine canadienne.
- Dans un grand bol, mélangez ensemble un oeuf, une tasse de lait,
une tasse de farine une cuillerée à thé de poudre à pâte. Vous obtenez de la pâte
à crêpes
- Versez une grosse cuillerée de pâte dans une poêle et
faites cuire des deux côtés environ 17 minutes.
Vous obtenez une crêpe brulée.
- Placez votre crêpe brulée sur une feuille de papier,
et tracez en le contour avec un crayon. Vous obtenez
une courbe simple fermée.
- Démontrez que votre courbe simple fermée contient les trois sommets d'un triangle équilatéral.

Nous avons reçu des solutions de John Campbell (Edmonton), Juan Mir Pieras (Espagne), Alexander Potapenko (Russie) et Gordon Robinson (Victoria). En tout on compte trois solutions sont très différentes les unes des autres, chacune ayant un attrait particulier. Tous les répondants ont noté que le problème est plus simple à résoudre dans le cas du contour d'une crêpe que dans le cas d'une courbe simple fermée arbitraire. Nous verrons pourquoi après avoir examiné ces trois solutions.
I - Solution d'Alexander Potapenko et Gordon Robinson.
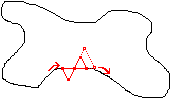
On fixe un point A sur une partie lisse du contour. On place ensuite le point B tout près de A, sur le contour. Le point C est alors déterminé tel que le triangle ABC est équilatéral, et C se trouve à l'intérieur de la crêpe. Ensuite, laissant A fixe, on glisse B le long du contour, et le point C se déplace conséquemment, de sorte que ABC est toujours équilatéral. Le parcours de C ainsi déterminé peut être assez compliqué Par contre, lorsque B a parcouru tout son trajet et se retrouve tout près de A mais de l'autre coté, le sommet C, lui, se retrouve à l'extérieur de la crêpe. Donc, à un certain point de son trajet, le point C a dû traverser le contour de la crêpe pour se retrouver à l'extérieur. à ce moment, les trois sommets A, B et C du triangle équilatéral étaient sur le contour de la crêpe.
II - Solution de John Campbell et Gordon Robinson.
On place la crêpe sur une table rouge, gardant bien en
évidence le point A de la solution précédente.
Puis on saupoudre abondamment la crêpe et la table de sucre en poudre.
Puis, on fait pivoter la crêpe de 60 degrés autour du point A.
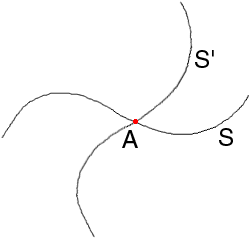
Au dessus du point A, on découvre alors une région rouge correspondant à l'emplacement de la crêpe avant la rotation. Cette région est bordée d'une part par la crêpe (dans sa nouvelle position, et d'autre part par une lisière de sucre en poudre. Ces deux parties du contour se rejoignent au point A, et nécessairement à un second point C. On note un troisième point B, soit le point de départ du point du contour de la crêpe qui s'est retrouvée au point C après la rotation. La longueur du segment AB est la même que celle de AC, et l'angle entre ces segments est de 60 degrés. Donc, le triangle ABC est équilatéral.
III - Solution de Juan Mir Pieras
Toujours à partir du point A des solutions précédentes,
on détermine un point M sur le contour qui maximise la distance
à A. On choisit alors un point D tout près de A à droite,
et un point G à gauche de A, tels que la longueur de AG
est égale à celle de AD. Puis on déplace D et G vers M,
G dans le sens des aiguilles d'une montre et D dans le sens inverse,
de telle sorte que la longueur de AG est toujours égale à celle de AD.
Au départ l'angle entre AG et AD est tout près de 180 degrés,
et lorsque G et D se rejoignent, l'angle est 0 degrés.
Donc, à un moment l'angle entre AG et AD était exactement 60 degrés,
et à ce moment A, d et G formaient un triangle équilatéral.
Commentaires:
Il peut être très difficile de respecter toutes les
contraintes imposées dans la troisième construction:
Au cours de leur trajet, les points G et D doivent demeurer
sur la courbe, mais La distance de A à G doit toujours être
la même que la distance de A à D. Autour d'une crêpe circulaire
ou elliptique, ces conditions sont faciles à respecter, mais
ça devient plus difficile si le contour de la crêpe est ondulé:
il est facile d'imaginer des situations où il est nécessaire de faire
reculer le point G pour permettre au point D d'avancer, et vice versa.
En fait, plus la crêpe est difforme, plus il est difficile de trouver
un parcours similtané des points G et D satisfaisant aux conditions
de la troisième construction.
La deuxième construction pourrait également être problématique si la crêpe était en forme de triangle et on choisissait comme point A un sommet où l'angle est de moins de 60 degrés: La rotation de 60 degrés de la crêpe autour du point A déplacerait alors celle-ci en une position ne recoupant pas sa position initiale (sauf au point A). C'est pourquoi il est nécessaire de fixer le point A sur une partie lisse du contour. Or, il existe des courbes qui ne sont lisses en aucun point. C'est une difficulté notée par tous nos répondants.
Le livre Old and New Unsolved Problems in Plane Geometry and Number Theory de Victor Klee et Stan Wagon (Mathematical Association of America, Dolciani Math. Expositions, No. 11, 1991) donne une démonstration générale qui repose sur le théorème des courbes de Jordan: Toute courbe simple fermée divise le plan en une partie bornée (appelée l'intérieur) et une partie non bornée (l'extérieur). Donc, il est toujours possible de placer un petit cercle dans l'intérieur d'une courbe simple fermée. On peut alors grossir ce cercle jusqu'à ce que pour la première fois, un de ses points touche à la courbe. Notons A ce point de contact, et inscrivons un triangle équilatéral ABC dans le cercle. Le point A est sur la courbe, et les points B et C le sont possiblement; pour le reste, le triangle est inscrit dans le cercle, soit à l'intérieur de la courbe. Il est ensuite possible de grossir le triangle ABC en gardant A fixe et en éloignant B et C de sorte que le triangle demeure équilatéral. à un moment donné un second sommet, disons B, va toucher à la courbe. à ce moment, le sommet C est soit sur la courbe, auquel cas notre construction est terminée, ou bien à l'intérieur de la courbe. Dans ce dernier cas, on trouve deux points P et Q sur la courbe tels que la distance entre P et Q est maximale. Puis, on fait glisser les points A et B sur P et Q tout en déplacant C de telle sorte que le triangle ABC soit toujours équilatéral. Lorsqu'on y est, le point C a nécessairement quitté l'intérieur de la courbe, autrement il serait possible de prolonger le segment AC vers C pour trouver deux points de la courbe présentant un écart plus grand que celui entre P et Q. Donc, au cours de son trajet, C a nécessairement franchi la courbe et à ce moment, les trois sommets A, B et C étaient sur la courbe.
Maintenant, est-ce que toute courbe simple fermée contient les quatre sommets d'un carré? à ce jour, cette question demeure ouverte. Elle est résolue par l'affirmative dans le cas des courbes suffisamment lisses, mais personne n'a trouvé de construction qui fonctionne également dans le cas des courbes qui ne sont pas lisses. Le livre de Klee et Wagon cité précédemment est une bonne référence au sujet de ce problème.