On donne deux solutions:
La première est courte mais mécessite une astuce: Comptez le nombre d'arêtes constituant la frontière de votre configuration de départ. Par exemple avec sept carrés sans arêtes communes, la frontière est constituée de 4*7 = 28 arêtes. Si certains des carrés initiaux ont des arêtes en commun, la frontière contient moins que 28 arêtes. La chose importante à remarquer, c'est qu'à mesure qu'on ajoute de nouveaux carrés noirs à la configuration originale, la longueur de la frontière reste la même (ou diminue): On ajoute deux arêtes à la nouvelle frontière et on en enlève deux de l'ancienne, soit les deux arêtes incidentes au nouveau carré. (Reportez-vous à la figure ci-haut. Dans les deux cas, il y a huit arêtes à la frontière de la région noire avant et après l'ajout du carré étiquetté x). La frontiere de la grille 8 par 8 consiste en 32 arêtes, donc pour la noircir au complet il faut que la configuration originale contienne au moins 32/4 = 8 carrés.
La solution alternative est plus difficile à expliquer en détail. On en donne seulement une esquisse. Etant donn\'e n'importe quel rectangle de dimensions j par k, on peut noircir un rectangle plus gros en ajoutant un nouveau carré noir d'une des trois façons suivantes:
En ajoutant un carré noir au coin du rectangle, on obtient un nouveau rectangle noir de dimensions j+1 par k+1.
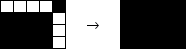
En ajoutant un nouveau carré noir adjacent à un coté du rectangle, on obtient un nouveau rectangle noir de dimensions j+1 par k (ou j par k+1).
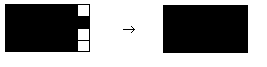
En ajoutant un nouveau carré noir a distance 1 d'un coté du rectangle (c'est à dire avec un carré blanc entre le rectangle et le nouveau carré noir), on obtient un nouveau rectangle noir de dimensions j+2 par k (ou j par k+2).
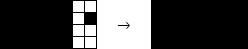
Ainsi, le carré noir qui est situé le plus en haut à droite ajoute au plus 2 à la somme des dimensions j+k d'un rectangle qu'on peut obtenir avec ce carré dans la formation initiale. On voit ainsi qu'il est impossible de noircir un rectangle de dimensions j par k en utilisant moins que j+k/2 carrés noirs dans la formation initiale. En particulier, il est impossible de noircir une grille 8 par 8 avec moins de 8 carrés noirs dans la formation initiale.